Mastering Linear Algebra for AI: A Guide to Vectors, Matrices, and Tensors

Introduction to Linear Algebra in AI

Linear algebra is the backbone of artificial intelligence (AI) and machine learning (ML). From representing data to performing complex computations, linear algebra provides the mathematical framework necessary for AI algorithms. Whether it’s transforming images in computer vision, optimizing weights in deep learning, or performing dimensionality reduction in data science, linear algebra plays a crucial role in AI applications.

In this guide, we’ll explore the fundamental concepts of linear algebra, including vectors, matrices, and tensors, and their significance in AI and ML.

Understanding Vectors: Representation and Operations

A vector is a fundamental mathematical entity in AI, often used to represent data points, features, or directions in space. Vectors can be visualized as points in multi-dimensional space and are widely used in fields like natural language processing (NLP) and recommendation systems.

1. Key Vector Operations:

Addition and Subtraction

Vectors can be added or subtracted component-wise. If we have two vectors:

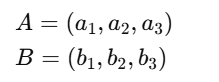
Then their sum is:

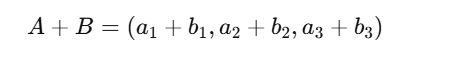
Similarly, subtraction is:

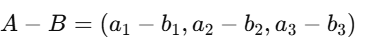
Practical Example: Suppose a self-driving car needs to compute its movement in a 2D space. If it moves 3 units forward and 4 units to the right (Vector A), and then another 2 units forward and 1 unit to the right (Vector B), the final position is given by adding both vectors:

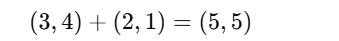
Scalar Multiplication

A vector can be scaled by multiplying it with a constant (scalar):

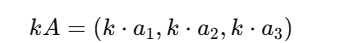
Practical Example: In image processing, brightness adjustments use scalar multiplication. Increasing brightness might involve multiplying the RGB color vector of each pixel by a scalar factor.

Dot Product

The dot product of two vectors is given by:

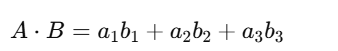
The dot product measures the similarity between two vectors.

Practical Example: In NLP, the similarity between words is determined using word embeddings (e.g., Word2Vec). If vectors representing the words "king" and "queen" have a high dot product, they are considered similar in meaning.

Cross Product

The cross product of two 3D vectors results in a new vector that is perpendicular to both:

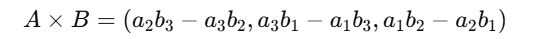
Practical Example: In computer graphics, cross products are used for calculating surface normals, which help determine how light interacts with a 3D object in rendering engines.

Norm (Magnitude of a Vector)

The norm (or length) of a vector is calculated as:

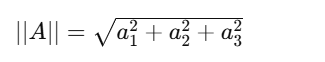
Practical Example: In optimization problems, such as gradient descent in machine learning, the norm of a gradient vector determines how large a step the model should take in parameter space.

Vectors enable AI systems to process and analyze multi-dimensional data efficiently, making them essential for tasks like document similarity, clustering, and classification.

More Information- Mathematics for Machine Learning: Linear Algebra Basics

Matrices in AI: Transformations, Inversions, and Multiplication

A matrix is a 2D array of numbers used extensively in AI for representing and manipulating data. From image processing to neural networks, matrices provide a structured way to perform mathematical operations efficiently.

1. Important Matrix Operations:

Matrix Addition and Subtraction

Matrices of the same dimensions can be added or subtracted element-wise:

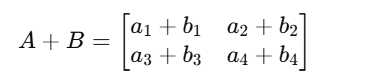
Practical Example: In AI, feature maps in Convolutional Neural Networks (CNNs) often involve element-wise addition during residual learning (ResNets) to improve deep learning models.

Matrix Multiplication

Matrix multiplication is crucial in AI, as it enables transformations and data representations. Given two matrices A and B :

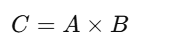
where each element Cij is computed as the dot product of the corresponding row in A and column in B .

Practical Example: In deep learning, weights in a neural network layer are stored as matrices. Forward propagation in a neural network involves matrix multiplications between input vectors and weight matrices to generate activations.

Matrix Inversion

The inverse of a matrix A is denoted as A-1, satisfying:

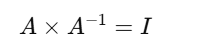
where I is the identity matrix.

Practical Example: In AI, matrix inversion is used in solving linear equations, such as in regression models for calculating optimal coefficients.

Determinant and Rank

The determinant of a square matrix helps in understanding its properties. If  det (A) = 0, the matrix is singular (non-invertible). The rank indicates the number of independent rows/columns.

Practical Example: In AI, Singular Value Decomposition (SVD), which relies on matrix rank, is used in recommender systems for collaborative filtering.

Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors help in dimensionality reduction. For a matrix A, an eigenvector v satisfies:

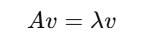
Practical Example: PCA (Principal Component Analysis), widely used in AI for reducing dimensionality while preserving important information, is based on eigenvalue decomposition.

In AI, matrices are essential for encoding datasets, transforming images, and performing multi-layered calculations in deep learning networks.

More Information- Mathematics for Machine Learning: Linear Algebra Basics

Understanding Tensors in AI: Theory and Practical Applications

Tensors are the fundamental data structures in artificial intelligence (AI) and deep learning. They represent multi-dimensional arrays, enabling efficient computation and manipulation of data. Let’s explore their theoretical concepts and practical applications.

1. Theoretical Understanding of Tensors

A tensor is a generalization of scalars (single numbers), vectors (1D arrays), and matrices (2D arrays) into higher dimensions. They are widely used in AI to store and process data efficiently.

1.2 Types of Tensors

1. Scalars (0D tensors)
   • A single numerical value, e.g., 5 or 3.14.
   • Represented as a tensor with zero dimensions.

   • Example in Python:

     import torch
     scalar = torch.tensor(5)
     print(scalar.ndim)  # Output: 0
     

2. Vectors (1D tensors)
   • A list of numbers, representing features, word embeddings, etc.
   • Example: [1.5, 2.3, -0.7]

   • Example in Python:

     vector = torch.tensor([1.5, 2.3, -0.7])
     print(vector.ndim)  # Output: 1
     

3. Matrices (2D tensors)
   • A 2D array used in transformations, convolutions, and neural networks.

   • Example:

     [[1, 2, 3], 
      [4, 5, 6]]
     

   • Example in Python:

     matrix = torch.tensor([[1, 2, 3], [4, 5, 6]])
     print(matrix.ndim)  # Output: 2
     

4. Higher-Dimensional Tensors (3D+ tensors)
   • Used for handling complex structures like images, videos, and time-series data.
   • Example:
     • 3D tensor for an RGB image: Height × Width × Channels (3)
     • 4D tensor for a batch of images: Batch × Height × Width × Channels

   • Example in Python:

     tensor_3D = torch.rand(3, 4, 5)  # 3x4x5 tensor
     print(tensor_3D.ndim)  # Output: 3
     

More Information- Mathematics for Machine Learning: Linear Algebra Basics

2. Practical Applications of Tensors in AI

2.1 Tensor Operations

Tensors support essential operations that form the backbone of deep learning:

1. Reshaping (Changing tensor shape)

   reshaped = matrix.reshape(3, 2)  # Changing 2x3 matrix to 3x2
   

2. Transposition (Swapping dimensions)

   transposed = matrix.T  # Transpose a matrix (swap rows & columns)
   

3. Element-wise operations (Addition, multiplication, etc.)

   tensor_1 = torch.tensor([1, 2, 3])
   tensor_2 = torch.tensor([4, 5, 6])
   sum_result = tensor_1 + tensor_2  # Element-wise addition
   

4. Matrix Multiplication (Essential for neural networks)

   matrix_A = torch.tensor([[1, 2], [3, 4]])
   matrix_B = torch.tensor([[5, 6], [7, 8]])
   product = torch.mm(matrix_A, matrix_B)  # Matrix multiplication
   

2.2 Tensors in Neural Networks

Deep learning frameworks like TensorFlow and PyTorch use tensors for:

1. Data Representation
   • Images as 4D tensors (Batch x Height x Width x Channels)
   • Text as embeddings in word vectors (1D or 2D tensors)
2. Training Neural Networks
   • Forward and backward propagation involve tensor operations like matrix multiplication, activation functions, and weight updates.

3. Gradient Computation (For optimization using backpropagation)

   x = torch.tensor(2.0, requires_grad=True)
   y = x**2
   y.backward()  # Compute gradient dy/dx
   print(x.grad)  # Output: 4.0
   

Practical Applications of Linear Algebra in Machine Learning

Linear algebra underpins numerous AI applications, including:

1. Computer Vision: Convolutional Neural Networks (CNNs) use matrix operations for image recognition and processing.
2. Natural Language Processing (NLP): Word embeddings, similarity measures, and topic modeling rely on vector and matrix representations.
3. Recommendation Systems: Matrices are used in collaborative filtering and matrix factorization techniques.
4. Dimensionality Reduction: PCA and Singular Value Decomposition (SVD) use eigenvectors and eigenvalues for feature extraction.
5. Optimization Algorithms: Gradient descent, which relies on matrix operations, is fundamental for training ML models.

Key Takeaways-

Linear algebra is a crucial component of AI and machine learning, providing the mathematical tools needed to process, transform, and optimize data. By understanding vectors, matrices, and tensors, AI practitioners can develop more efficient models and algorithms that power today’s intelligent systems. Whether you are working on deep learning, NLP, or computer vision, mastering linear algebra will significantly enhance your AI expertise.

 Next Blog- Calculus for AI (Derivatives, Gradients, and Optimization)