Probability Distributions and Bayes’ Theorem
Probability Distributions in AI: Normal, Binomial, and Poisson
Probability distributions are fundamental to AI and machine learning, helping models understand data patterns, make predictions, and optimize performance. This discussion covers three key probability distributions: Normal, Binomial, and Poisson, along with their theoretical background and practical applications.
1. Normal Distribution (Gaussian Distribution)
The normal distribution is a symmetric, bell-shaped curve where most data points cluster around the mean. It is defined by:
- Mean (μ): The central value of the dataset.
- Standard Deviation (σ): Indicates how spread out the data points are.
Formula:
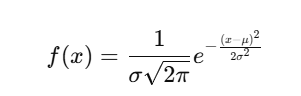
where:
- x is the data point,
- μ is the mean,
- σ is the standard deviation.
Characteristics:
- Symmetric around the mean.
- Follows the empirical rule: 68% of data within one standard deviation, 95% within two, and 99.7% within three.
Applications of Normal Distribution in AI
Neural Networks – Weight Initialization
- AI models initialize weights using a normal distribution for balanced training.
Image Processing – Gaussian Blur
- Normal distribution is used for image smoothing and noise reduction.
Anomaly Detection
- AI identifies outliers by measuring deviations from the mean.
Practical Example – Normal Distribution in Python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
mu, sigma = 0, 1 # Mean and Standard Deviation
data = np.random.normal(mu, sigma, 1000)
plt.hist(data, bins=30, density=True, alpha=0.6, color='b')
x = np.linspace(-4, 4, 100)
plt.plot(x, norm.pdf(x, mu, sigma), 'r', linewidth=2)
plt.title("Normal Distribution")
plt.show()
This visualization shows a bell-shaped curve, representing normally distributed data.
2. Binomial Distribution
The binomial distribution models binary (success/failure) outcomes over multiple trials. It is commonly used in classification problems where an event has two possible outcomes (e.g., spam/not spam).
Formula:
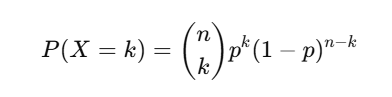
where:
- n = number of trials,
- k = number of successes,
- p = probability of success per trial.
Characteristics:
- Models events with two possible outcomes.
- Used in classification, A/B testing, and medical AI.
Applications of Binomial Distribution in AI
Spam Detection
- AI models classify emails as spam or not spam based on word frequencies.
Medical Diagnosis
- AI estimates the probability of a patient having a disease based on test results.
A/B Testing in Marketing
- AI analyzes conversion rates when testing two different webpage versions.
Practical Example – Binomial Distribution in Python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
n, p = 10, 0.5 # 10 trials, 50% probability of success
x = np.arange(0, n+1)
binomial_dist = binom.pmf(x, n, p)
plt.bar(x, binomial_dist, color='b', alpha=0.6)
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title("Binomial Distribution")
plt.show()
This bar chart represents the probability of achieving a specific number of successes over 10 trials.
3. Poisson Distribution
The Poisson distribution models the number of times an event occurs over a fixed interval (time or space) when events happen randomly.
Formula:
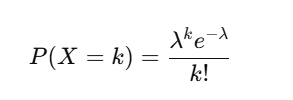
where:
- λ = average number of events per interval,
- k = number of occurrences,
- e = Euler's number.
Characteristics:
- Used for rare events occurring randomly over time.
- The mean and variance are both equal to λ\lambda.
Applications of Poisson Distribution in AI
Customer Arrivals in Queueing Systems
- AI predicts the number of customers arriving at a store within a time frame.
Fault Detection in Manufacturing
- AI models detect machine failures based on historical fault rates.
Traffic Flow Optimization
- AI analyzes the number of cars passing a signal per minute for smart traffic management.
Practical Example – Poisson Distribution in Python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
lambda_val = 5
x = np.arange(0, 15)
poisson_dist = poisson.pmf(x, lambda_val)
plt.bar(x, poisson_dist, color='b', alpha=0.6)
plt.xlabel("Number of Events")
plt.ylabel("Probability")
plt.title("Poisson Distribution")
plt.show()
4. Exponential Distribution
The exponential distribution models the time until the next event in a Poisson process (where events happen randomly over time).
Mathematical Formula
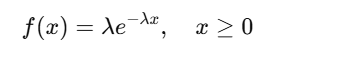
where:
- λ = rate of occurrences
Why It’s Important in AI
- Survival Analysis: Predicts the time until hardware failure in AI-powered maintenance systems.
- Queueing Theory: AI models use this to manage waiting times in call centers and optimize server load balancing.
Example in Python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon
# Generate exponential distribution
x = np.linspace(0, 10, 1000)
y = expon.pdf(x, scale=1)
# Plot the distribution
plt.plot(x, y, 'r')
plt.title("Exponential Distribution")
plt.show()
5. Uniform Distribution
In the uniform distribution, every outcome is equally likely. It is often used in random sampling and Monte Carlo simulations.
Mathematical Formula
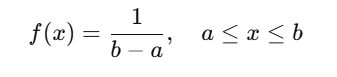
where:
- a,b = range of values
Why It’s Important in AI
- Randomized Algorithms: Used in Monte Carlo simulations for decision-making.
- Data Shuffling: AI uses uniform distribution to randomly select training samples in machine learning models.
Example in Python
import numpy as np
import matplotlib.pyplot as plt
# Generate uniform distribution
data = np.random.uniform(0, 10, 1000)
# Plot the distribution
plt.hist(data, bins=30, density=True, alpha=0.6, color='c')
plt.title("Uniform Distribution")
plt.show()
| Distribution | Use Case in AI |
|---|---|
| Normal | Neural network weight initialization, noise modeling |
| Binomial | Binary classification, A/B testing |
| Poisson | Event prediction, anomaly detection |
| Exponential | Time until failure, queueing models |
| Uniform | Monte Carlo simulations, data shuffling |
The Power of Bayes’ Theorem in AI and Predictive Analytics
Bayes’ Theorem is a key principle in probability theory that helps AI models make better predictions by updating prior knowledge as new information becomes available. It plays a crucial role in machine learning, decision-making, and predictive analytics.
Understanding Bayes’ Theorem
Bayes’ Theorem is mathematically expressed as:
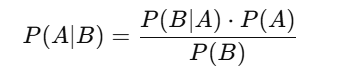
Where:
- P(A∣B) = Posterior probability (Updated probability of event AAA after observing event BBB)
- P(B∣A) = Likelihood (Probability of observing event BBB given that AAA is true)
- P(A) = Prior probability (Initial belief about event AAA before seeing BBB)
- P(B) = Marginal probability (Total probability of event BBB occurring)
Why Bayes’ Theorem Matters in AI
1. Predictive Analytics and Decision Making
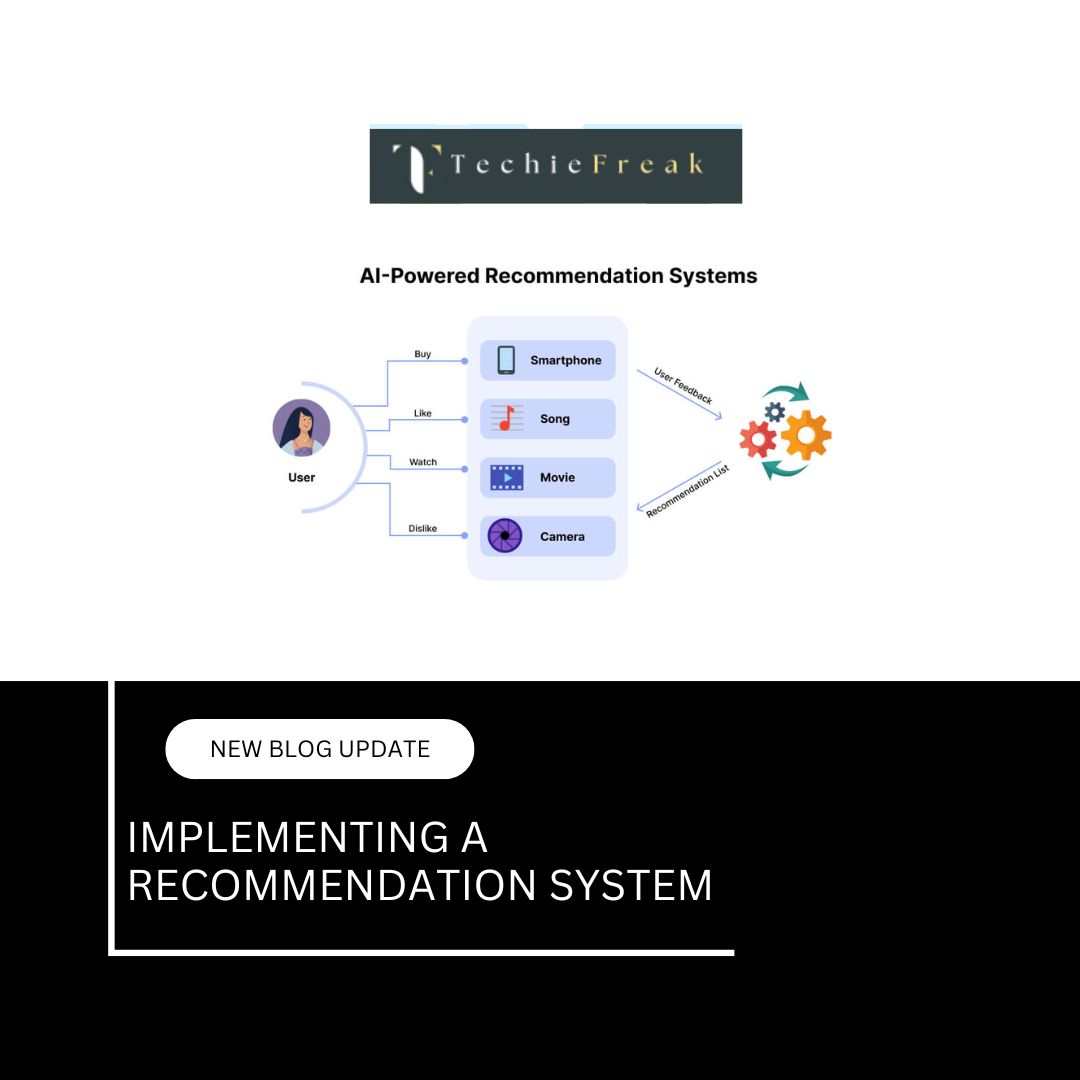
Bayes’ Theorem helps AI systems refine predictions based on real-time data. For example, recommendation engines use Bayesian models to suggest content based on user behavior.
2. Spam Detection in Emails
Email filters use Naïve Bayes classifiers, a machine learning technique based on Bayes' Theorem, to determine whether an email is spam by analyzing words in the subject and body.
3. Medical Diagnosis
AI-driven healthcare systems use Bayesian inference to update disease probabilities based on symptoms and test results, improving diagnosis accuracy.
4. Fraud Detection
Bayesian models help detect fraudulent transactions by updating risk assessments based on new transaction patterns.
5. Natural Language Processing (NLP)
Bayesian models are used in text classification and sentiment analysis to determine the likelihood of certain words appearing in different contexts.
Example: Spam Classification Using Bayes' Theorem
Imagine you receive an email containing the word "lottery." You want to determine whether the email is spam or not.
Given:
- P(Spam) = 0.3 (30% of emails are spam)
- P(Ham) = 0.7 (70% of emails are not spam)
- P("lottery" | Spam) = 0.8 (80% of spam emails contain "lottery")
- P("lottery" | Ham) = 0.1 (10% of non-spam emails contain "lottery")
Applying Bayes’ Theorem:
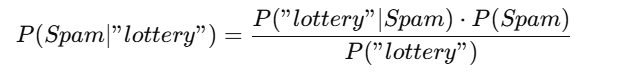
Where:
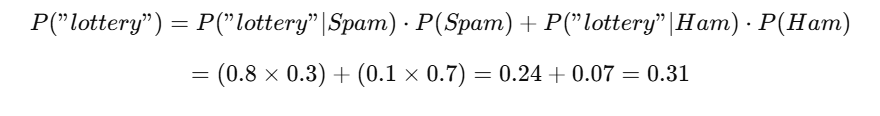
Now:
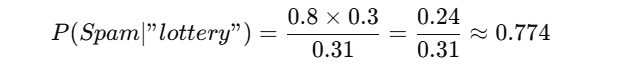
So, the probability that the email is spam given that it contains "lottery" is 77.4%.
Python Implementation of Naïve Bayes for Spam Detection
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
# Sample training data
emails = ["Win a lottery now", "Meeting at 10 AM", "Claim your free prize", "Project deadline extended"]
labels = [1, 0, 1, 0] # 1 = spam, 0 = ham
# Convert text to numerical feature vectors
vectorizer = CountVectorizer()
X_train = vectorizer.fit_transform(emails)
# Train Naïve Bayes model
model = MultinomialNB()
model.fit(X_train, labels)
# Test on new email
test_email = ["Congratulations! You won a free lottery"]
X_test = vectorizer.transform(test_email)
# Predict spam or not
prediction = model.predict(X_test)
print("Spam" if prediction[0] == 1 else "Not Spam")Practical Examples of Bayes’ Theorem in AI Applications
- Natural Language Processing (NLP): S
- entiment analysis, topic modeling, and spam detection rely on probabilistic reasoning using Bayes' Theorem.
- Computer Vision: Object detection and recognition models use Bayesian updating for improved accuracy.
- Fraud Detection: AI systems assess the probability of fraudulent transactions based on past data.
- Recommendation Systems: Platforms like Netflix and Amazon predict user preferences using Bayesian modeling.
By understanding probability distributions and Bayes’ Theorem, AI practitioners can build robust models capable of making accurate predictions in uncertain environments.
Key Takeaways: Probability Distributions and Bayes’ Theorem in AI
1. Probability Distributions in AI
- Normal Distribution (Gaussian): Used for neural network weight initialization, image processing, and anomaly detection.
- Binomial Distribution: Models binary outcomes (e.g., spam detection, medical diagnosis, A/B testing).
- Poisson Distribution: Predicts event occurrences over a fixed interval (e.g., customer arrivals, fault detection, traffic flow).
- Exponential Distribution: Models time until the next event in a Poisson process (e.g., hardware failure prediction, queueing systems).
- Uniform Distribution: Ensures equal probability for all outcomes (e.g., Monte Carlo simulations, data shuffling).
2. Bayes’ Theorem in AI
- Formula: Updates probabilities based on new evidence.
- Applications:
- Predictive Analytics: Improves recommendations and decision-making.
- Spam Detection: Naïve Bayes classifier filters emails.
- Medical Diagnosis: AI refines disease probability based on symptoms and test results.
- Fraud Detection: Detects anomalies in financial transactions.
- Natural Language Processing: Powers sentiment analysis and text classification.
By leveraging probability distributions and Bayes' Theorem, AI models enhance predictive accuracy and optimize decision-making in real-world applications.
Next Blog- Graph Theory and AI
.png)




.jpg)










.jpg)


.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)

.png)