1. What is Spectral Clustering?

Spectral Clustering is an algorithm that performs clustering based on the spectrum (eigenvalues) of a similarity matrix. It is particularly useful when the dataset contains clusters that are not necessarily spherical or linearly separable in high-dimensional space.

The basic idea is to transform the problem of clustering into a graph partitioning problem and then solve this problem using eigenvalues and eigenvectors.

2. Steps in Spectral Clustering

The general steps involved in Spectral Clustering are:

Step 1: Construct a Similarity Graph

The first step in Spectral Clustering is to construct a similarity graph that represents the relationships or similarities between data points. This graph forms the basis for grouping similar data points into clusters. Here's a more detailed breakdown of this step:

1.1 What is a Similarity Graph?

A Similarity Graph is a graph where:

• Nodes (vertices) represent individual data points from the dataset.
• Edges between nodes represent the similarity or relationship between the data points.

The weight of the edge between two nodes indicates the strength of the similarity between the corresponding data points.

Key Points:

• The graph is undirected, meaning if data point i is similar to j, then j is also similar to i.
• The graph can be sparse or dense, depending on the similarity threshold and the size of the dataset.

1.2 Creating the Similarity Matrix (W)

The Similarity Matrix (W) is a square matrix that stores the similarity values between all pairs of data points. For a dataset X with n data points, the similarity matrix W is an n×n matrix, where each element Wij represents the similarity between data points i and j.

Properties of the Similarity Matrix:

• It is typically symmetric: Wij=Wji
• The diagonal elements Wii​ are often set to zero (no self-similarity), but sometimes they can be set to a value representing self-similarity (e.g., 1).

1.3 How is Similarity Measured?

There are several ways to compute the similarity between two data points, but the most common methods are:

1.3.1 Gaussian (RBF) Kernel:

One of the most widely used similarity measures is the Gaussian Radial Basis Function (RBF) Kernel, which measures similarity based on the Euclidean distance between two data points.

For two points xi and xj​, the similarity Wij​ is computed as:

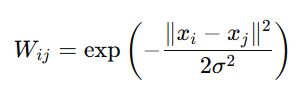
Where:

• ∥xi−xj∥2  is the squared Euclidean distance between the two points.
• σ is a parameter that controls the width of the kernel (how far the influence of one point reaches). A small value of σ makes the kernel more sensitive, resulting in stronger similarity between points that are close to each other.
• The value of Wij will be closer to 1 for similar points and closer to 0 for dissimilar points.

Interpretation:

• Large similarity (Wijj​ close to 1) means the points are similar (close in space).
• Small similarity (Wij​ close to 0) means the points are dissimilar (far apart).

1.3.2 K-Nearest Neighbors (K-NN) Similarity:

Another common method is using K-Nearest Neighbors (K-NN) to construct the similarity matrix. Here's how it works:

• For each data point xi​, find its K nearest neighbors based on a distance metric (e.g., Euclidean distance).
• The similarity between two points xi​ and xj​ is set to a non-zero value if xj is among the K-nearest neighbors of xi.
• The matrix is sparse, with only the non-zero elements corresponding to the neighbors.

Interpretation:

• Similarity between points is only defined if they are neighbors, and it is often set to a fixed value (e.g., 1 for neighbors, 0 for non-neighbors).

Step 2: Compute the Laplacian Matrix

After constructing the similarity graph (Step 1), the next step in spectral clustering is to compute the Laplacian matrix. The Laplacian matrix is a key concept in graph theory and plays a central role in spectral clustering. It captures the structure of the graph, helping to understand the relationships and connectivity between nodes, and is used to identify clusters.

2.1 What is the Laplacian Matrix?

The Laplacian matrix is a square matrix that describes the connectivity of a graph. For a graph with n nodes, the Laplacian matrix L is an n×n matrix.

The Laplacian matrix is defined as:

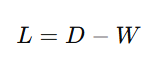
Where:

• D is the degree matrix.
• W is the similarity matrix (constructed in Step 1).

2.2 Degree Matrix (D)

The degree matrix D is a diagonal matrix, where each element Dii represents the degree of the i-th node. The degree of a node is the sum of the weights of all edges connected to that node.

• Unweighted Graph: If the graph is unweighted, the degree Dii is simply the number of edges connected to the node i.
• Weighted Graph: If the graph is weighted, the degree Dii is the sum of the weights of the edges connected to node i.

Mathematically, the degree of node i is:

Where Wij​ is the element from the similarity matrix representing the weight between nodes i and j.

2.3 Similarity Matrix (W)

The similarity matrix W is the matrix representing the edges in the graph, where each element Wij corresponds to the similarity (or weight) between nodes i and j. This matrix is computed in Step 1 using a similarity measure (like the Gaussian kernel or K-NN).

2.4 Computing the Laplacian Matrix (L)

Once the degree matrix D and similarity matrix W are known, the Laplacian matrix L is computed as:

L=D−W

This matrix captures the difference between the degree of each node and its actual connections (based on the similarity matrix). The diagonal elements of L contain information about the degree of each node, while the off-diagonal elements contain information about the relationships between nodes (similarities).

2.5 Importance of the Laplacian Matrix in Spectral Clustering

The Laplacian matrix plays an important role in spectral clustering because it captures the graph's connectivity and is used to discover clusters in the data. Here’s why it is important:

2.5.1 Captures Graph Structure:

• The Laplacian matrix L encodes information about the structure of the graph (i.e., how nodes are connected and how strongly).
• This helps to understand the relationships between data points, which is essential for identifying clusters.

2.5.2 Eigenvalues and Eigenvectors Reveal Clusters:

• The eigenvalues and eigenvectors of the Laplacian matrix are central to spectral clustering.
• The smallest eigenvalues (often associated with the Fiedler vector) help identify the number of clusters and the cluster assignments.
• The eigenvectors corresponding to the smallest eigenvalues (especially the second smallest, known as the Fiedler vector) help in the partitioning of the graph into clusters.

2.5.3 Handles Non-Linearity:

• Spectral clustering, using the Laplacian matrix, can handle non-linear clusters that other algorithms like k-means cannot, because it operates on the graph structure rather than the original feature space.

2.5.4 Robust to Noise:

• Spectral clustering can be more robust to noise compared to other algorithms, as the graph can represent the underlying structure even if some data points are outliers.

2.6 Normalized Laplacians

In some cases, a normalized Laplacian matrix is used instead of the unnormalized one. Normalization is often applied to improve the performance of spectral clustering, especially in cases where the graph is very large or unbalanced.

Normalized Laplacian:

The normalized Laplacian matrix can be defined in different ways, but the most common forms are:

Symmetric Normalized Laplacian:

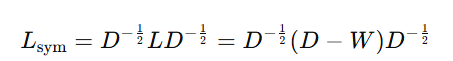
• This form normalizes the Laplacian by taking the square root of the degree matrix on both sides.

Random Walk Normalized Laplacian:

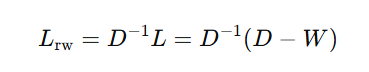
• This normalization is useful in random walk-based clustering algorithms.

Why Use Normalized Laplacian?

• Normalization can stabilize the computation and improve convergence.
• It helps to balance clusters when the graph's degree distribution is highly skewed.

Step 3: Compute Eigenvectors

In Step 3 of spectral clustering, the goal is to compute the eigenvectors of the Laplacian matrix (L), which will help in identifying the clusters.

1. Eigenvalue Decomposition: Perform an eigenvalue decomposition of the Laplacian matrix L (or its normalized versions). This means solving the equation Lv=λv , where v is the eigenvector and λ is the eigenvalue.
2. Select k Eigenvectors: Choose the first k eigenvectors corresponding to the smallest eigenvalues. These eigenvectors contain the most important information about the graph's structure.
   • For the unnormalized Laplacian, the smallest eigenvalues (including the zero eigenvalue) are used.
   • For the normalized Laplacian, the smallest eigenvalues provide a better representation of the data structure.
3. Cluster Representation: The eigenvectors corresponding to these eigenvalues define the structure of the data and can be used to form clusters.

By using these eigenvectors, we can reduce the data's dimensionality, and each point can be represented by the corresponding values of the selected eigenvectors. Then, these values are used to cluster the points using traditional clustering methods (like k-means).

Step 4: Form a New Matrix

• Stack Eigenvectors: After selecting the first k eigenvectors from the previous step, stack them together to form a new matrix X, where each row represents an eigenvector, and each column corresponds to the component of the eigenvector for each data point.
• Normalize Rows: Normalize each row of this matrix X to make them unit vectors (i.e., vectors with a length of 1). This step ensures that the data points represented by the eigenvectors are on a comparable scale.
• This new matrix X is now ready for the next step, where clustering algorithms (like k-means) will be applied to find the final clusters.

Step 5: Clustering

• Apply a standard clustering algorithm (usually K-means) on the rows of the eigenvector matrix. These rows can be considered as points in a lower-dimensional space that reflects the structure of the original data.

3. Why Spectral Clustering Works

Spectral Clustering works well because it is based on the graph Laplacian, which captures the connectivity of the data points. The eigenvectors of the Laplacian matrix reveal the underlying structure of the data, even when the clusters are non-convex or have arbitrary shapes.

The algorithm can uncover clusters by finding the natural divisions in the graph (i.e., where the similarity between points is high) based on the eigen-decomposition.

4. Properties of Spectral Clustering

• Non-linearity: Spectral Clustering can find clusters that are not linearly separable, making it very powerful for complex datasets.
• Flexible Similarity Measures: You can use different similarity measures (Gaussian kernel, cosine similarity, etc.) to capture the relations between data points.
• Sensitivity to Parameters: The algorithm depends on the choice of similarity function and the value of k, the number of clusters. Inappropriate values can lead to poor performance.
• Efficient for Large Datasets: While computationally intensive, particularly the eigenvalue decomposition, techniques like approximate spectral clustering have been developed for scalability.

5. Applications of Spectral Clustering

Spectral Clustering is applicable in a wide range of domains, including:

• Image segmentation: Partitioning images into regions based on pixel similarity.
• Social networks: Grouping users based on their interactions.
• Genetics and bioinformatics: Grouping genes or biological data points that share common properties.
• Dimensionality reduction: Reducing high-dimensional data to lower dimensions while preserving important structure.

6. Advantages of Spectral Clustering

• Captures Complex Cluster Structures: Can identify clusters with non-convex shapes.
• No Assumptions about Cluster Shape: Unlike K-means, spectral clustering doesn't assume that clusters are spherical or isotropic.
• Works Well with Similarity Graphs: It excels in domains where data can naturally be represented as a graph (e.g., social networks, data with proximity or relational features).

7. Limitations of Spectral Clustering

• Computational Complexity: The algorithm requires computing the eigenvalues and eigenvectors of the Laplacian matrix, which can be expensive for large datasets.
• Choice of Similarity Measure: The results are highly dependent on the choice of the similarity measure. If the similarity function does not capture the true structure of the data, it may lead to incorrect clustering.
• Requires Predefined Number of Clusters: Spectral Clustering typically requires the number of clusters to be specified in advance, like K-means. However, techniques like the eigengap heuristic can help in selecting k. 

8. Mathematical Overview of Spectral Clustering

Given the graph G=(V,E)G = (V, E)G=(V,E) where V is the set of vertices (data points) and E is the set of edges (similarity relationships), spectral clustering involves the following steps:

• Construct a similarity matrix W, which is the adjacency matrix of the graph.

• Compute the degree matrix D,
   

  

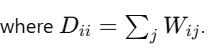
• Compute the Laplacian matrix L=D−W or a normalized version.
• Find the eigenvectors corresponding to the smallest eigenvalues of L.
• Cluster the rows of the eigenvector matrix using a classical clustering algorithm like K-means.

9. Variants of Spectral Clustering

• Normalized Spectral Clustering: A more advanced approach uses the normalized Laplacian matrix Lsym​ or Lrw​ to make the algorithm more robust to variations in data scale.
• Approximate Spectral Clustering: For large datasets, approximations like Nystrom method or randomized algorithms can be used to speed up the computation.
• Multi-scale Spectral Clustering: Uses spectral clustering at different scales, allowing the algorithm to adapt to datasets with varying cluster densities.

Key Takeaways-

1. What is Spectral Clustering?
   • A clustering algorithm based on the spectrum (eigenvalues) of a similarity matrix.
   • Effective for non-linearly separable or complex clusters.
2. Steps in Spectral Clustering:
   • Step 1: Construct a Similarity Graph – Represent data points as nodes, with edges showing similarity (Gaussian kernel or K-NN).
   • Step 2: Compute Laplacian Matrix – Captures graph structure using degree and similarity matrices.
   • Step 3: Compute Eigenvectors – Eigenvalues/eigenvectors of the Laplacian help identify clusters.
   • Step 4: Form a New Matrix – Stack selected eigenvectors, normalize rows, and prepare for clustering.
   • Step 5: Clustering – Use clustering algorithms like K-means on the eigenvector matrix.
3. Why It Works:
   • The Laplacian matrix captures connectivity, revealing the natural structure of the data for clustering.
4. Properties:
   • Handles non-convex clusters.
   • Flexible with similarity measures.
   • Sensitive to similarity function choice and number of clusters.
5. Applications:
   • Image segmentation, social networks, bioinformatics, and dimensionality reduction.
6. Advantages:
   • Identifies complex, non-convex cluster structures.
   • No assumption about cluster shape.
7. Limitations:
   • Computationally expensive for large datasets.
   • Highly dependent on similarity measure and predefined cluster number.
8. Variants:
   • Normalized, approximate, and multi-scale spectral clustering for scalability and robustness.

Next Blog-  Python Implementation of Spectral Clustering