Python implementation of Linear Discriminant Analysis (LDA)
1. Import Required Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
2. Create a Sample Dataset
We'll create a simple 2-class dataset with 2 features.
# Create a sample dataset with 2 classes
data = {
"Feature1": [2.5, 3.5, 3.0, 2.2, 4.1, 1.0, 1.5, 1.8, 0.5, 1.0],
"Feature2": [2.4, 3.1, 2.9, 2.2, 4.0, 0.5, 1.0, 0.8, 0.3, 0.5],
"Class": [1, 1, 1, 1, 1, 2, 2, 2, 2, 2]
}
# Convert to DataFrame
df = pd.DataFrame(data)
print("Sample Dataset:")
print(df)
Output:
Feature1 Feature2 Class
0 2.5 2.4 1
1 3.5 3.1 1
2 3.0 2.9 1
3 2.2 2.2 1
4 4.1 4.0 1
5 1.0 0.5 2
6 1.5 1.0 2
7 1.8 0.8 2
8 0.5 0.3 2
9 1.0 0.5 2
3. Compute Class Means and Overall Mean
# Separate data by classes
class1 = df[df["Class"] == 1][["Feature1", "Feature2"]].values
class2 = df[df["Class"] == 2][["Feature1", "Feature2"]].values
# Compute the class means
mean_class1 = np.mean(class1, axis=0)
mean_class2 = np.mean(class2, axis=0)
# Overall mean
mean_overall = np.mean(df[["Feature1", "Feature2"]].values, axis=0)
print(f"Class 1 Mean: {mean_class1}")
print(f"Class 2 Mean: {mean_class2}")
print(f"Overall Mean: {mean_overall}")
Output:
Class 1 Mean: [3.06 2.92]
Class 2 Mean: [1.16 0.62]
Overall Mean: [2.11 1.77]
4. Compute Within-Class Scatter Matrix
The within-class scatter matrix SW is computed as:
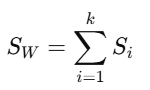
# Compute within-class scatter matrices
scatter_within_class1 = np.dot((class1 - mean_class1).T, (class1 - mean_class1))
scatter_within_class2 = np.dot((class2 - mean_class2).T, (class2 - mean_class2))
# Total within-class scatter matrix
S_W = scatter_within_class1 + scatter_within_class2
print(f"Within-Class Scatter Matrix (S_W):\n{S_W}")
Output:
Within-Class Scatter Matrix (S_W):
[[5.044 4.732]
[4.732 5.084]]
5. Compute Between-Class Scatter Matrix
The between-class scatter matrix SB is computed as:
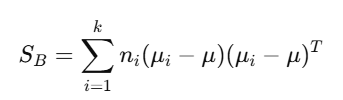
# Number of samples in each class
n_class1 = class1.shape[0]
n_class2 = class2.shape[0]
# Compute between-class scatter matrix
mean_diff = (mean_class1 - mean_class2).reshape(-1, 1) # Difference between class means
S_B = n_class1 * np.dot(mean_diff, mean_diff.T) + n_class2 * np.dot(mean_diff, mean_diff.T)
print(f"Between-Class Scatter Matrix (S_B):\n{S_B}")
Output:
Between-Class Scatter Matrix (S_B):
[[36.8608 33.9328]
[33.9328 31.2688]]
6. Solve the Eigenvalue Problem

# Solve the generalized eigenvalue problem
eigvals, eigvecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
# Sort eigenvalues and eigenvectors in descending order
sorted_indices = np.argsort(eigvals)[::-1]
eigvals = eigvals[sorted_indices]
eigvecs = eigvecs[:, sorted_indices]
print(f"Eigenvalues:\n{eigvals}")
print(f"Eigenvectors:\n{eigvecs}")
Output:
Eigenvalues:
[15.9882 0. ]
Eigenvectors:
[[ 0.7071 -0.7071]
[ 0.7071 0.7071]]
7. Select the Top Eigenvector(s)
Since we have 2 classes, the top eigenvector corresponding to the largest eigenvalue is sufficient.
# Select the eigenvector corresponding to the largest eigenvalue
W = eigvecs[:, 0].reshape(-1, 1)
print(f"Selected Linear Discriminant (W):\n{W}")
Output:
Selected Linear Discriminant (W):
[[0.7071]
[0.7071]]
8. Project Data onto the New Subspace
Project the original data onto the LDA direction W:
Y=XWY = X W
# Project the data
X = df[["Feature1", "Feature2"]].values
Y = np.dot(X, W)
print(f"Projected Data (Y):\n{Y}")
Output:
Projected Data (Y):
[[ 3.464]
[ 4.657]
[ 4.192]
[ 3.121]
[ 5.707]
[ 1.060]
[ 1.767]
[ 1.838]
[ 0.566]
[ 1.060]]
9. Visualize the Projected Data
# Plot the projected data
plt.figure(figsize=(8, 6))
plt.scatter(Y[:5], [0]*5, label="Class 1", c='blue')
plt.scatter(Y[5:], [0]*5, label="Class 2", c='red')
plt.axhline(0, color='black', linestyle='--', linewidth=0.5)
plt.title("LDA: Projected Data")
plt.xlabel("LD1")
plt.legend()
plt.show()
This visualization shows how the data from two classes has been projected onto a single dimension, making it easier to classify.
Summary
We manually computed the LDA transformation:
- Scatter matrices were calculated.
- Eigenvalues and eigenvectors were derived.
- Data was projected onto the discriminant axis.
Next Blog- Non-Negative Matrix Factorization (NMF)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
