Principal Component Analysis (PCA)

Principal Component Analysis (PCA) is a statistical technique used for dimensionality reduction while preserving as much variance (information) in the data as possible. It is often used in exploratory data analysis and for making predictive models. PCA helps simplify the complexity in high-dimensional data by transforming it into a smaller number of variables, called principal components. These components are new axes that capture the most significant variance in the data.

Key Concepts of PCA

1. Dimensionality Reduction:
   • Dimensionality refers to the number of features (or variables) in a dataset. In high-dimensional datasets, the number of features can be overwhelming, and finding meaningful patterns becomes challenging.
   • PCA reduces the number of dimensions without losing much information, making data easier to visualize and process while improving the performance of machine learning algorithms.
2. Variance and Information:
   • The principal components are ranked according to the amount of variance they capture. The first principal component (PC1) captures the most variance, the second principal component (PC2) captures the second most variance, and so on.
   • By using the first few principal components, we can represent the data with minimal loss of information.
3. Orthogonality of Principal Components:
   • The principal components are orthogonal (i.e., they are at right angles to each other) and uncorrelated. This means each component captures unique variance that is independent of the others.
4. Eigenvalues and Eigenvectors:
   • PCA is based on eigenvalue decomposition of the covariance matrix of the data.
     • Eigenvalues represent the magnitude of the variance captured by each principal component.
     • Eigenvectors represent the direction of the principal components.
   • The eigenvalues determine how much information (variance) each eigenvector (principal component) contains. Higher eigenvalues correspond to principal components that capture more variance.

Steps of PCA

Step 1: Standardize the Data

If the data features have different units or scales (e.g., height in cm, weight in kg), we need to standardize the data. Standardization ensures each feature contributes equally to the analysis by scaling each feature to have a mean of 0 and a standard deviation of 1.

The standardization formula is:

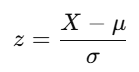
where:

• X is the original data point.
• μ is the mean of the feature.
• σ is the standard deviation of the feature.

Step 2: Compute the Covariance Matrix

The covariance matrix represents how the features of the data relate to one another. It’s a square matrix that shows the covariance between each pair of features.

• For two features X and Y, the covariance is computed as:

  

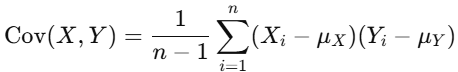
  where:

• n is the number of data points.
• μX​ and μY​ are the means of X and Y, respectively.
• The covariance matrix is symmetric, and its diagonal elements represent the variances of individual features.

Step 3: Compute the Eigenvalues and Eigenvectors

Once we have the covariance matrix in PCA, the next step is to perform eigenvalue decomposition to obtain the eigenvalues and corresponding eigenvectors.

Eigenvectors:

• Definition: Eigenvectors represent the direction of the new principal axes in the dataset.
• Interpretation: These directions correspond to the axes along which the data has the most variance. In simpler terms, eigenvectors tell us the orientations in which the data points are spread out the most.

Eigenvalues:

• Definition: Eigenvalues represent the magnitude of the variance along the direction of each eigenvector.
• Interpretation: The eigenvalue indicates how much variance exists in the data along the corresponding eigenvector's direction. Higher eigenvalues mean more variance in that direction, while smaller eigenvalues indicate less variance. These values help to identify the most important dimensions of the data.

The higher the eigenvalue, the more important that eigenvector (direction) is for explaining the data's variability. By selecting the top eigenvectors with the largest eigenvalues, PCA reduces the dimensionality of the data while retaining the most important features.

The eigenvectors are the principal components, and the eigenvalues indicate how much variance each component captures.

Step 4: Sort Eigenvalues and Select Top Principal Components

In this step, we aim to select the most important principal components based on the variance explained by each component. The top principal components are the directions in which the data varies the most, and they are associated with the largest eigenvalues.

How to Select Top Principal Components:

1. Sort the Eigenvalues:
   • The first step is to sort the eigenvalues in decreasing order. This way, we can identify which principal components explain the most variance in the data.
2. Select Corresponding Eigenvectors:
   • Once the eigenvalues are sorted, we select the eigenvectors (which represent the directions of maximum variance) corresponding to these eigenvalues.
3. Choose the Number of Principal Components:
   • We then decide how many of the top principal components to retain. This is typically based on the cumulative variance explained by the selected components.
   • For instance, if we want to retain 95% of the total variance, we keep adding principal components (starting from the one with the largest eigenvalue) until the cumulative explained variance reaches the desired threshold.
   • Practical Example:

   • If you have 3 eigenvalues sorted as follows: 4.5, 1.2, 0.7, you might decide to keep the first two principal components if their cumulative variance (e.g., 4.5 + 1.2 = 5.7) accounts for, say, 95% of the total variance, and discard the third one.

     In essence, the Top Principal Components are the most significant directions (or axes) of the data, with the highest eigenvalues indicating the most important dimensions of variability. These are the components that will form your reduced feature space after dimensionality reduction through PCA.

What are the Top Principal Components?

• The top principal components are the eigenvectors associated with the largest eigenvalues.
• These eigenvectors represent the directions in which the data varies the most, and selecting them helps reduce the dimensionality of the dataset while retaining most of the information.

Step 5: Project the Data onto the New Principal Components

Finally, we transform the original dataset by projecting it onto the selected principal components. This step reduces the dimensionality of the dataset while retaining the most significant variance.

Mathematically, the projection is achieved by multiplying the standardized data by the matrix of the selected eigenvectors (principal components).

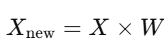
where:

• Xnew​ is the transformed dataset with fewer dimensions.
• W is the matrix of the selected eigenvectors.

Applications of PCA

1. Dimensionality Reduction:
   • PCA is widely used to reduce the dimensionality of high-dimensional datasets. For example, in image processing, where each image can have thousands of pixels (features), PCA can reduce the number of pixels while preserving the important features.
2. Data Visualization:
   • PCA helps in visualizing high-dimensional data. By reducing the data to two or three dimensions, it can be plotted, helping to identify patterns and clusters that might not be obvious in higher dimensions.
3. Noise Reduction:
   • By removing the components with the least variance (which may correspond to noise), PCA can help denoise data and improve the performance of subsequent algorithms.
4. Preprocessing for Machine Learning:
   • PCA is used as a preprocessing step before feeding data into machine learning algorithms, particularly for algorithms that suffer from the curse of dimensionality (e.g., k-nearest neighbors, support vector machines).
5. Face Recognition:
   • PCA is used in face recognition, where high-dimensional image data is transformed into a lower-dimensional space to help with efficient comparisons between faces.
6. Anomaly Detection:
   • PCA can also be used for anomaly detection by analyzing how much of the variance each data point contributes. Points that deviate significantly from the main distribution (low variance) are often considered anomalies.

Advantages of PCA

1. Reduces Overfitting: By reducing the dimensionality of the dataset, PCA can help reduce overfitting, especially when the number of features is large.
2. Improves Efficiency: Reducing the number of features can make machine learning models faster to train and test, as fewer computations are required.
3. Captures Most Information: PCA retains the most important features (those that capture the most variance), reducing complexity without significant loss of information.
4. Helps in Data Visualization: It allows high-dimensional data to be visualized in 2D or 3D plots.

Disadvantages of PCA

1. Loss of Interpretability: The transformed features (principal components) are linear combinations of the original features, making them hard to interpret. This can be a drawback if feature interpretability is crucial.
2. Sensitive to Scaling: PCA is sensitive to the scale of the data. If the features are not standardized, features with larger ranges will dominate the results.
3. Linear Assumption: PCA assumes linear relationships between features. It may not perform well with datasets that have non-linear relationships.
4. Computationally Expensive: The computation of eigenvectors and eigenvalues can be expensive for large datasets.

Key Takeaways:

1. Dimensionality Reduction:
   • PCA reduces the number of features in a dataset, making high-dimensional data easier to visualize, interpret, and process without significant information loss.
2. Variance Preservation:
   • The goal of PCA is to preserve the most significant variance in the data. Principal components are ranked by how much variance they explain, with the first principal component (PC1) capturing the most variance.
3. Eigenvectors and Eigenvalues:
   • Eigenvectors represent the directions (or axes) along which the data varies the most.
   • Eigenvalues determine the amount of variance captured by each eigenvector. Larger eigenvalues correspond to more important principal components.
4. Orthogonality:
   • The principal components are orthogonal, meaning they are uncorrelated and each captures unique variance, providing a new basis for the data.
5. Selecting Top Principal Components:
   • PCA involves sorting eigenvalues in decreasing order and selecting the corresponding eigenvectors that capture the most variance. The number of components is chosen based on a desired cumulative variance threshold (e.g., 95%).
6. Data Transformation:
   • After selecting the top principal components, the data is projected onto these components to reduce its dimensionality while retaining the most important information.
7. Applications of PCA:
   • Dimensionality Reduction: Used to simplify high-dimensional datasets, such as in image processing.
   • Data Visualization: Helps visualize high-dimensional data by reducing it to 2D or 3D.
   • Noise Reduction: Helps remove less significant components, which might correspond to noise, improving data quality.
   • Preprocessing for Machine Learning: Reduces dimensionality for better performance of algorithms.
   • Anomaly Detection: Identifies outliers by analyzing variance and deviations from normal patterns.
8. Advantages of PCA:
   • Reduces overfitting by simplifying the data.
   • Improves computational efficiency by reducing feature space.
   • Retains the most informative components for further analysis.
   • Helps in visualizing high-dimensional data in lower dimensions.
9. Disadvantages of PCA:
   • Loss of interpretability due to transformed features being linear combinations of original features.
   • Sensitive to data scaling—features must be standardized for accurate results.
   • Assumes linear relationships, making it unsuitable for datasets with non-linear patterns.
   • Can be computationally expensive for very large datasets.

Next Blog- Principal Component Analysis (PCA) Using Python