Python Implementation of DBSCAN using Scikit-Learn

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a density-based clustering algorithm that groups together closely packed points while marking points in low-density regions as outliers. Unlike other clustering algorithms like K-Means, DBSCAN doesn't require the number of clusters to be specified in advance. Instead, it defines clusters based on the density of points, which makes it well-suited for data with irregular shapes and noise.

DBSCAN works by identifying regions of high point density and separating them from regions of low density (outliers). It is particularly useful when clusters have arbitrary shapes and are unevenly distributed.

Key Parameters of DBSCAN:

• eps: The maximum distance between two points for them to be considered as in the same neighborhood.
• min_samples: The minimum number of points required to form a dense region (cluster).
• metric: The distance metric to use for calculating the distance between points (Euclidean is the default).
• algorithm: The algorithm used for computing nearest neighbors (auto, ball_tree, kd_tree, brute).
• leaf_size: The leaf size for the ball tree or kd-tree (useful for large datasets).

Steps for Python Implementation of DBSCAN:

1. Import Necessary Libraries
2. Prepare the Data
3. Apply DBSCAN
4. Visualize the Clusters
5. Evaluate the Results

Step-by-Step Code with Explanations:

Step 1: Import Necessary Libraries

We'll start by importing the necessary libraries: numpy, pandas, scikit-learn for model building, and matplotlib for visualization.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN

Step 2: Prepare the Data

We can either use real data or generate synthetic data. For this example, we'll generate some synthetic data using make_blobs.

• make_blobs: Used to generate synthetic data (optional in real use cases).
• DBSCAN: The DBSCAN class from sklearn.cluster to apply DBSCAN clustering.
• matplotlib.pyplot: For plotting the results.

# Generating random dataset with 3 clusters
X, _ = make_blobs(n_samples=300, centers=3, random_state=42)
print(X[:5])

OUTPUT:
[[-7.33898809 -7.72995396]
 [-7.74004056 -7.26466514]
 [-1.68665271  7.79344248]
 [ 4.42219763  3.07194654]
 [-8.91775173 -7.8881959 ]]

• n_samples=300: Generates 300 data points.
• centers=3: The data will have 3 centers (clusters).
• random_state=42: Ensures reproducibility of the results.

Alternatively, you can use your real dataset.

Step 3. Data Pre-processing for Clustering

Before building the model, we need to pre-process the data. In this preprocessing step, we focus on following steps:

• Missing Value Imputation, here we just remove the missing value if any feature has by its median or Mode.
• Drop the columns which is not impacting the target
• Visualize the relationship between the feature to check if they are highly corelated to each other.
• Check if there is any categorical feature, remove it to numerical feature by applying OHE (One Hot Encoding).

Here in this example, we are not doing the pre-processing.

Step 4: Apply DBSCAN

Now that we have our data, let's apply DBSCAN for clustering.

# Applying DBSCAN
dbscan = DBSCAN(eps=0.5, min_samples=5)
y_dbscan = dbscan.fit_predict(X)
print(y_dbscan)

OUTPUT:
[ 0  0  2  1 -1  1  2  1  2  2 -1  1  2  2  0  2  0 -1  2 -1  2  2  1  0
  2  3  0 -1  1  2  2  2  0  2 -1  2  0  1  0  1  1  2  0  1  2  2  0  1
  0 -1  1 -1  0 -1  0 -1  0  2  1  2  0 -1  1 -1  0  1  1  0  0  2  1 -1
  0  2  2  0  0  1  2  1  2  2  0  2  1  0  0 -1 -1  4  0  2  0  2  2  0
  0  2  0  3  1  2  1  2  2  2  2  2 -1  0 -1  2  2  2  2  1  0 -1  0 -1
  1  1 -1  0  0  0  0  2  0  0  2  2  2 -1 -1  1  1  0  2  0  2  2 -1  2
  1  1  1  2  1  2  4  0  1 -1  2  1  1  0 -1  2 -1  0  0  0  2  0  1 -1
  2  2  2 -1  1  2  1  1  1 -1 -1  1  0  2  0 -1  1 -1  1 -1 -1  1  0 -1
  1  0  1 -1  1 -1  2  0  2  2  1  1  2  1  0  0  1  2  2  0  1 -1  0  0
  3  0  4 -1 -1 -1  0  0  2  1  0  0  1  2 -1 -1  2 -1  1  1  0  1  0  0
  3  1  1  2  0  1  1  1  0  1  0  1  0 -1 -1  0  1  2 -1  2  2  2  0  2
  1  1  0  1  1  2  2  1  1  1  0  0  0  4 -1  4  1  1 -1 -1  0  1 -1  1
  1  0  2  1  1  2  0  2  1  2  3 -1]

• eps=0.5: This is the maximum distance between two points to be considered neighbours. It means two points must be within 0.5 units of each other to belong to the same cluster.
• min_samples=5: Minimum number of points required to form a cluster. If fewer than 5 points are within the distance defined by eps, they are considered noise.
• fit_predict(X): Fits the DBSCAN model to the data and predicts the cluster labels for each point. The result y_dbscan contains cluster labels for each data point.

Step 4: Visualize the Clusters

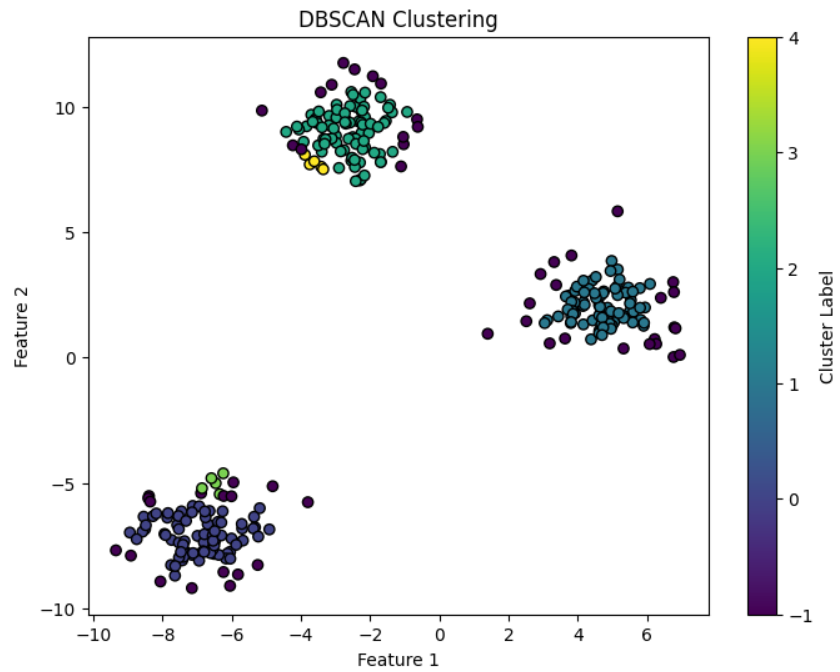
Now, let’s visualize the clusters created by DBSCAN.

# Plotting the DBSCAN clusters
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_dbscan, cmap='viridis', marker='o', edgecolor='k')
plt.title("DBSCAN Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.colorbar(label='Cluster Label')
plt.show()

• X[:, 0] and X[:, 1]: Extracting the first and second features from the dataset for plotting.
• c=y_dbscan: The y_dbscan array contains cluster labels, so each point is colored according to its assigned cluster.
• cmap='viridis': Color map for the clusters.
• marker='o': Marker style for the points.
• colorbar(): Adds a color bar to indicate the cluster labels.

OUTPUT:

Step 5: Evaluate the Results

The fit_predict function returns cluster labels for each point. Points that are classified as noise by DBSCAN are labeled as -1. Let's evaluate the results.

# Number of clusters (excluding noise)
num_clusters = len(set(y_dbscan)) - (1 if -1 in y_dbscan else 0)
print(f"Number of clusters (excluding noise): {num_clusters}")

# Number of noise points
num_noise_points = list(y_dbscan).count(-1)
print(f"Number of noise points: {num_noise_points}")


OUTPUT:
Number of clusters (excluding noise): 5
Number of noise points: 52

• set(y_dbscan): The unique values in y_dbscan, which represent the cluster labels. The label -1 indicates noise points.
• num_clusters: The number of clusters, excluding noise points (-1).
• num_noise_points: The number of noise points (those labeled as -1).

Full Code Example:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN

# Step 1: Generate synthetic data
X, _ = make_blobs(n_samples=300, centers=3, random_state=42)

# Step 2: Apply DBSCAN
dbscan = DBSCAN(eps=0.5, min_samples=5)
y_dbscan = dbscan.fit_predict(X)

# Step 3: Visualize the clusters
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_dbscan, cmap='viridis', marker='o', edgecolor='k')
plt.title("DBSCAN Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.colorbar(label='Cluster Label')
plt.show()

# Step 4: Evaluate the results
num_clusters = len(set(y_dbscan)) - (1 if -1 in y_dbscan else 0)
print(f"Number of clusters (excluding noise): {num_clusters}")
num_noise_points = list(y_dbscan).count(-1)
print(f"Number of noise points: {num_noise_points}")

Explanation of DBSCAN Results:

• Noise Points: Any data points that do not have enough neighbors to form a cluster are labeled as -1. These points are considered outliers or noise.
• Clusters: Points with the same cluster label (other than -1) belong to the same cluster. DBSCAN will merge points that are close to each other into the same cluster, even if they don't form compact shapes.

Tuning DBSCAN Parameters:

• eps: If eps is too small, too many points will be considered noise. If eps is too large, too many points may be merged into one cluster.
• min_samples: If min_samples is too high, DBSCAN may not be able to form clusters and mark too many points as noise. Conversely, if min_samples is too low, DBSCAN may merge too many points into one cluster.

Conclusion:

DBSCAN is a powerful clustering algorithm, especially for data with noise and irregularly shaped clusters. Unlike K-Means, it doesn't require specifying the number of clusters in advance and can discover outliers effectively. However, it requires tuning the eps and min_samples parameters to perform well on different datasets.