Data Normalization and Standardization in Machine Learning
In the realm of machine learning, data preprocessing plays a pivotal role in ensuring that the data fed into machine learning algorithms is structured, clean, and ready for model training. Among the various data preprocessing techniques, data normalization and standardization are the two most commonly used methods for scaling numerical features. These techniques help in transforming the data into a suitable format, improving the performance and stability of machine learning algorithms.
In this in-depth blog, we will thoroughly explore the concepts of data normalization and standardization, their differences, use cases, and practical implementations.
1. What is Data Normalization?
Data normalization refers to the process of rescaling feature values into a specific range, typically [0, 1] or [-1, 1], without distorting differences in the ranges of values. The primary purpose of normalization is to ensure that features are on a comparable scale and have an equal contribution to the model. This is especially important when using algorithms that rely on distance calculations or gradient-based optimization techniques.
Mathematical Concept:
Normalization often uses the Min-Max Scaling method, which is defined as:
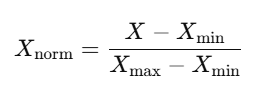
Where:
- X is the original value of the feature.
- Xmin and Xmax are the minimum and maximum values of that feature in the dataset.
- Xnorm is the normalized value of the feature.
This formula transforms the data into a specific range, usually [0, 1], where:
- The minimum value of the feature is mapped to 0.
- The maximum value of the feature is mapped to 1.
- The other values are proportionally distributed between these two extremes.
When to Use Normalization?
Normalization is particularly useful when:
- The dataset has features with different scales: If one feature, such as "age," ranges from 20 to 100, and another feature, such as "income," ranges from 1000 to 10000, normalization can bring these features to the same scale.
- Distance-based algorithms are used, such as K-Nearest Neighbors (KNN), Support Vector Machines (SVM), and neural networks. These algorithms rely on calculating the distance between points (like Euclidean distance), and having features on different scales could cause the model to be biased towards features with larger numerical values.
- The data is not normally distributed: Normalization does not assume any specific distribution of the data, making it more flexible in handling various data distributions.
- You are using optimization algorithms: Gradient-based optimization algorithms, such as Gradient Descent in neural networks, benefit from normalized data as it ensures faster and more efficient convergence.
Practical Example of Normalization:
Let's say we have a dataset of "Age" and "Income." We will normalize the data to the [0, 1] range.
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
# Sample data
data = {'Age': [25, 30, 35, 40, 45], 'Income': [1000, 1500, 2000, 2500, 3000]}
df = pd.DataFrame(data)
# Create MinMaxScaler object
scaler = MinMaxScaler()
# Normalize the data
df_normalized = scaler.fit_transform(df)
print(df_normalized)
Output:
[[0. 0. ]
[0.25 0.25]
[0.5 0.5 ]
[0.75 0.75]
[1. 1. ]]
_1736346815.png)
Here, both "Age" and "Income" are scaled to the [0, 1] range, allowing them to contribute equally to distance-based algorithms.
2. What is Data Standardization?
Data standardization, also known as Z-score normalization, is the process of rescaling data such that it has a mean of 0 and a standard deviation of 1. Standardization is typically used when the data is normally distributed or when the algorithm assumes the data follows a normal distribution.
Mathematical Concept:
Standardization transforms data by subtracting the mean and dividing by the standard deviation:
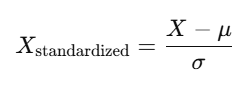
Where:
- X is the original value of the feature.
- μ is the mean of the feature in the dataset.
- σ is the standard deviation of the feature in the dataset.
- X Standardized is the standardized value of the feature.
This transformation centers the data around 0, with a spread of 1 standard deviation.
When to Use Standardization?
Standardization is recommended when:
- The algorithm assumes a normal distribution: Models like linear regression, logistic regression, and principal component analysis (PCA) assume that the data is normally distributed, and standardization ensures that the data fits this assumption.
- The dataset is continuous and not bound to a specific range, making the feature spread and scale essential for proper functioning of certain algorithms.
- You need to deal with outliers: Standardization is less sensitive to outliers than normalization because the mean and standard deviation are more robust to extreme values. However, extreme outliers can still impact the distribution.
- The data has varying scales: Standardization makes the data more suitable for models that are based on covariance and variance, like Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA).
Practical Example of Standardization:
Let's consider the same dataset of "Age" and "Income," but this time, we'll standardize the data.
from sklearn.preprocessing import StandardScaler
import pandas as pd
# Sample data
data = {'Age': [25, 30, 35, 40, 45], 'Income': [1000, 1500, 2000, 2500, 3000]}
df = pd.DataFrame(data)
# Create StandardScaler object
scaler = StandardScaler()
# Standardize the data
df_standardized = scaler.fit_transform(df)
print(df_standardized)
Output:
[[-1.41421356 -1.41421356]
[-0.70710678 -0.70710678]
[ 0. 0. ]
[ 0.70710678 0.70710678]
[ 1.41421356 1.41421356]]
_1736346850.png)
In this case, both "Age" and "Income" are standardized, resulting in a mean of 0 and a standard deviation of 1 for each feature.
3. Key Differences Between Normalization and Standardization
| Criteria | Normalization | Standardization |
|---|---|---|
| Purpose | Rescale the data to a fixed range (e.g., [0, 1]) | Center the data with a mean of 0 and unit variance |
| Method | Min-Max Scaling (based on min and max) | Z-Score Scaling (based on mean and standard deviation) |
| Range of Transformed Values | Typically [0, 1] or [-1, 1] | No fixed range, data can be any real number |
| Use Case | KNN, neural networks, distance-based algorithms | Linear regression, logistic regression, PCA |
| Assumption about Data Distribution | No assumptions about the distribution of data | Assumes the data is normally distributed (or close to it) |
| Sensitivity to Outliers | Sensitive to outliers (outliers can distort the scaling) | Less sensitive, but still affected by extreme outliers |
| Data Type | Useful for non-Gaussian, skewed, or bounded data | Useful for normally distributed or continuous data |
4. When Should You Use Each Technique?
- Normalization should be used when:
- You need to ensure that all features are on the same scale and contribute equally to the model.
- The dataset includes features with different units or magnitudes.
- You are using algorithms that rely on distances between points, such as KNN, SVM, and neural networks.
- Standardization should be used when:
- Your dataset follows a normal distribution (or close to it), which is common in many real-world datasets.
- The algorithm you are using assumes that the data has a mean of 0 and a standard deviation of 1, such as linear regression, logistic regression, and PCA.
- You are working with models that are sensitive to the covariance of features, such as PCA or LDA.
5. Practical Considerations
- Dealing with Test Data: When applying normalization or standardization, it’s crucial to fit the scaler only on the training data and apply the same transformation to the test data. This prevents information leakage from the test data during the training phase, which could lead to biased results.
- Handling Outliers: While standardization is less sensitive to outliers than normalization, extremely large outliers can still influence the mean and standard deviation. In such cases, it’s often useful to detect and handle outliers before applying any scaling techniques.
- Feature Engineering: In some cases, you may need to apply both normalization and standardization depending on the nature of the data and the model. For example, a neural network may require normalization of input features, while the output feature may need to be standardized.
Key Takeaways
Both normalization and standardization are essential techniques for scaling data in machine learning. While they serve the same goal — adjusting the scale of the features — the choice of technique depends on the type of data and the machine learning model you are using. By understanding the differences and appropriate use cases for each technique, you can enhance your model’s performance and ensure better results.
By carefully applying these preprocessing steps, you lay the foundation for building robust, efficient, and accurate machine learning models.
Next Topic : Splitting data into training and testing sets




.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
