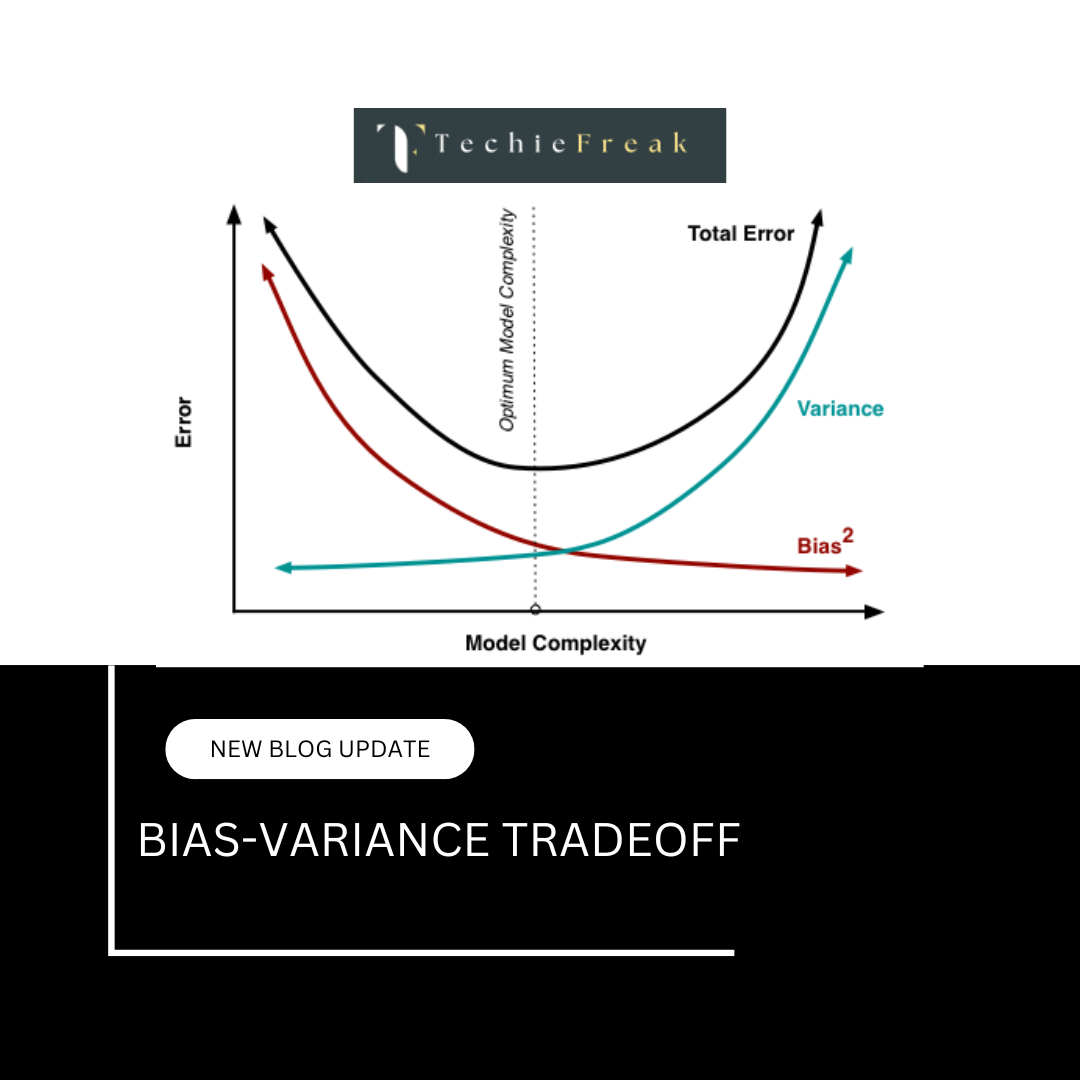
Bias-Variance Tradeoff: The Key to Building Generalizable Models

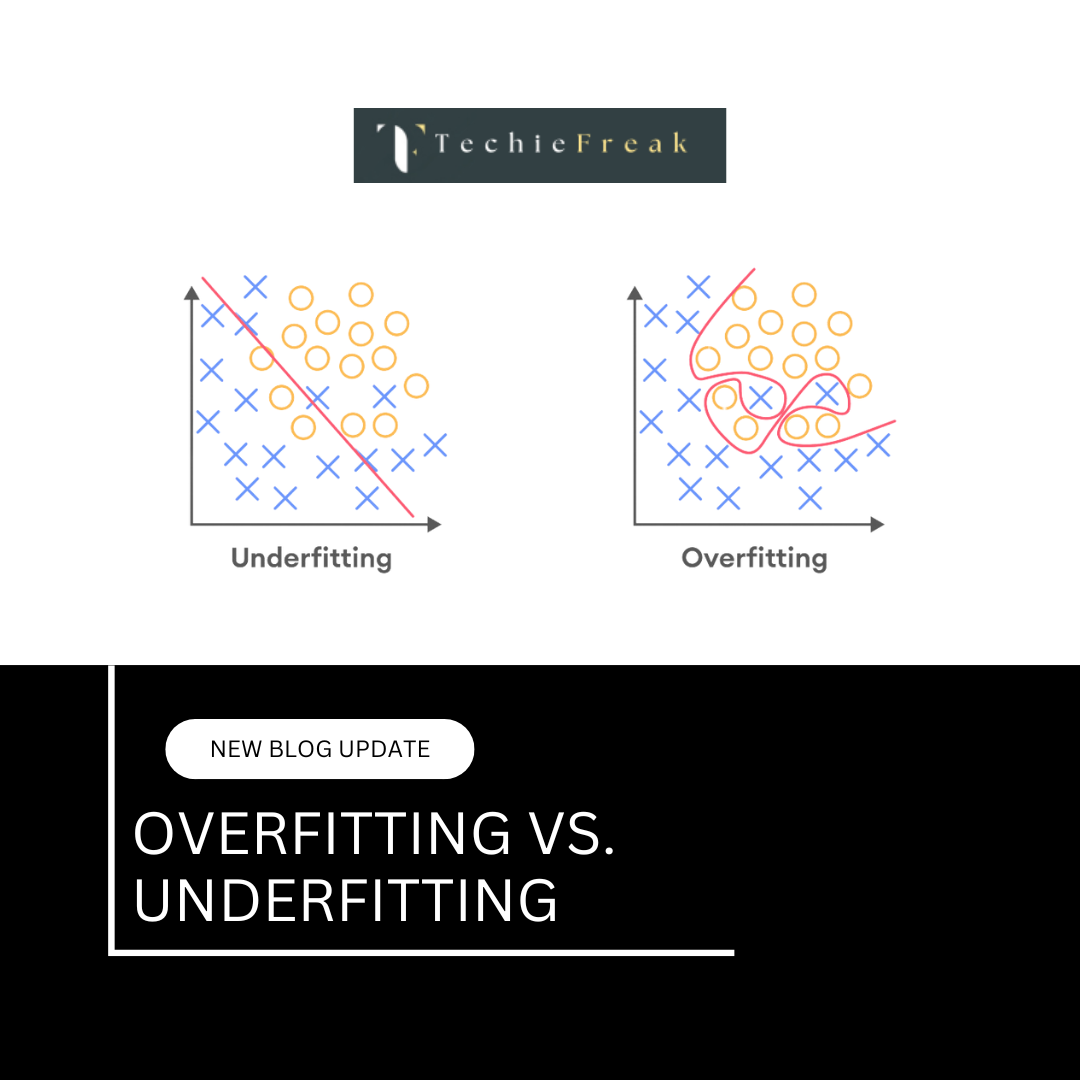
One of the fundamental challenges in machine learning is balancing bias and variance to create models that generalize well to unseen data. If a model is too simple, it may fail to capture important patterns in the data, leading to high bias (underfitting). On the other hand, if a model is too complex, it may memorize noise and variations in the training data, resulting in high variance (overfitting). This dilemma is known as the bias-variance tradeoff.

In this blog, we will explore bias and variance, understand their impact on model performance, and discuss strategies to achieve the right balance for building robust machine-learning models.

Understanding Bias and Variance in Machine Learning

1. What is Bias?

Bias refers to the error introduced by approximating a real-world problem with a simplified model. High bias means that the model makes strong assumptions about the data and may fail to learn key relationships.

Characteristics of High Bias Models:

• Oversimplifies the data
• Ignores important patterns
• Performs poorly on both training and test sets

Example of High Bias: Consider using linear regression to model a complex nonlinear relationship. The model may fail to capture the curvature and relationships in the data, leading to underfitting.

Mathematical Representation: The error due to bias can be expressed as:

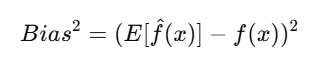
2. What is Variance?

Variance refers to the model’s sensitivity to fluctuations in the training data. A high-variance model captures noise in the dataset, leading to poor generalization.

Characteristics of High Variance Models:

• Overly complex models
• Captures noise instead of actual patterns
• Performs well on training data but poorly on unseen test data

Example of High Variance: Using a high-degree polynomial regression on a dataset may lead to excessive curve fitting, causing the model to perform poorly on new data.

Mathematical Representation: Variance is given by:

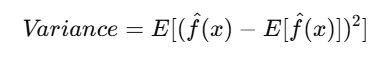
which measures the variability of model predictions.

Bias-Variance Tradeoff Explained with Examples

1. The Tradeoff Concept

The bias-variance tradeoff states that reducing bias often increases variance and vice versa. The goal is to find an optimal balance where the model captures important patterns while avoiding overfitting.

Illustration:

• High Bias, Low Variance: A simple model like linear regression that generalizes but underfits.
• Low Bias, High Variance: A complex model like deep neural networks that overfits to training data.
• Optimal Balance: A model that captures key patterns without memorizing noise.

2. Real-Life Analogy

Imagine you are learning to shoot arrows at a target:

• High Bias: All arrows land far from the center in a consistent pattern.
• High Variance: Arrows land all over the target with no consistent pattern.
• Optimal Model: Arrows cluster around the target’s center with slight variation.

How to Reduce High Bias (Underfitting)

When a model has high bias, it lacks complexity and cannot capture key relationships in the data. Here’s how to address underfitting:

1. Increase Model Complexity

• Move from linear regression to polynomial regression.
• Use more sophisticated models like decision trees or neural networks.

2. Train for a Longer Duration

• For deep learning, increase the number of epochs.
• Allow models to learn from the data longer.

3. Reduce Regularization

• L1/L2 regularization penalizes complexity, but too much can cause underfitting.
• Reduce lambda (penalty term) in models like Ridge and Lasso regression.

4. Improve Feature Engineering

• Add more relevant features that provide meaningful insights.
• Transform data using polynomial features or interactions.

5. Increase Training Data

• More diverse data helps models learn better representations.
• This is particularly useful in neural networks and deep learning.

How to Reduce High Variance (Overfitting)

When a model has high variance, it becomes too sensitive to training data. Here’s how to address overfitting:

1. Apply Regularization

• Use L1 Regularization (Lasso Regression) to remove irrelevant features.
• Use L2 Regularization (Ridge Regression) to reduce large coefficients.
• For deep learning, use Dropout to randomly disable neurons.

2. Use Cross-Validation

• k-Fold Cross-Validation ensures model performance is validated across multiple data splits.
• Helps detect overfitting early in training.

3. Prune Decision Trees

• Remove unnecessary branches to reduce complexity.
• Use post-pruning to improve generalization.

4. Reduce Model Complexity

• If using high-degree polynomials, try a lower degree.
• In neural networks, reduce the number of layers and neurons.

5. Use More Training Data

• More data helps the model generalize better and reduces variance.
• Data Augmentation can be used for images and text datasets.

Role of Training Data Size in Bias-Variance Tradeoff

Training data size plays a crucial role in managing the bias-variance tradeoff:

1. Small Dataset Challenges

• High variance due to lack of generalization.
• The model may memorize training data and fail on test data.

2. Large Dataset Benefits

• Helps reduce variance by exposing the model to more patterns.
• Reduces overfitting, especially for deep learning models.

3. Data Augmentation

• If more data isn’t available, augment it using transformations (image/text-based).
• Helps improve model generalization and mitigate overfitting.

Finding the Optimal Balance

Achieving the best tradeoff requires experimentation. Some practical steps include:

• Using learning curves to analyze performance.
• Performing hyperparameter tuning (e.g., adjusting regularization strength).
• Applying ensemble learning (bagging, boosting) to reduce variance.

Key Takeaways:

Understanding and managing the bias-variance tradeoff is critical for building machine learning models that generalize well. A well-balanced model should:

• Have a low bias to capture meaningful patterns.
• Have low variance to generalize to unseen data.
• Use proper training techniques to optimize learning.

By leveraging techniques such as regularization, cross-validation, and feature engineering, we can create models that perform well across different datasets. Balancing bias and variance is the key to achieving high model accuracy and reliability in real-world applications! 

Next Blog- Grid Search and Random Search for Hyperparameter Tuning