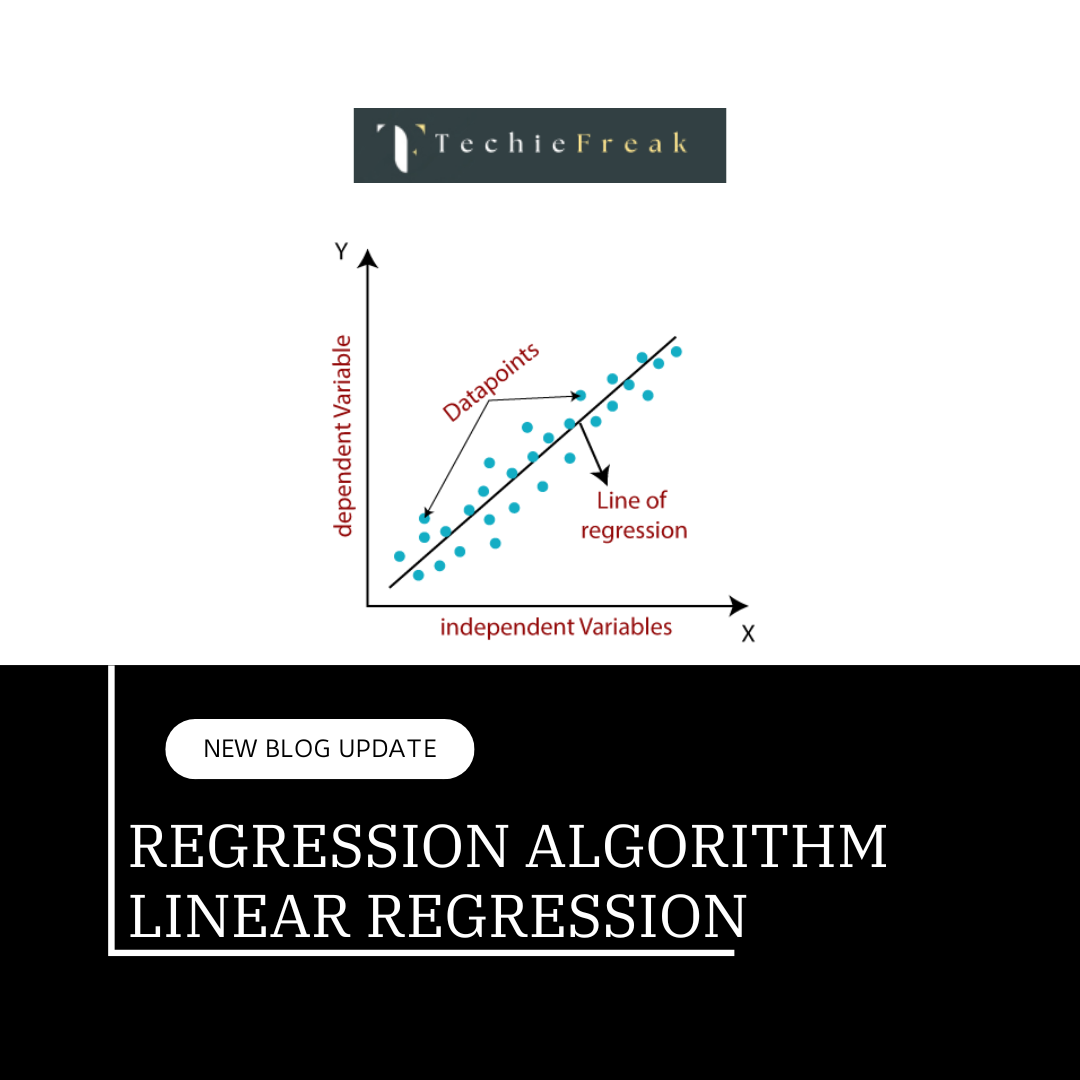
Lasso Regression, short for Least Absolute Shrinkage and Selection Operator, is a type of linear regression that performs regularization to improve model performance and interpretability. Regularization helps to prevent overfitting by adding a penalty term to the cost function of linear regression. Lasso uses L1 regularization, which minimizes the sum of the absolute values of the coefficients, effectively shrinking some of them to zero. This characteristic makes Lasso Regression useful for feature selection, as it can eliminate irrelevant features from the model.

The bias-variance tradeoff is a fundamental concept in machine learning and statistics, and it is particularly relevant in Lasso Regression. Lasso (Least Absolute Shrinkage and Selection Operator) is a regression technique that includes L1 regularization, which adds a penalty equivalent to the absolute value of the magnitude of the coefficients.

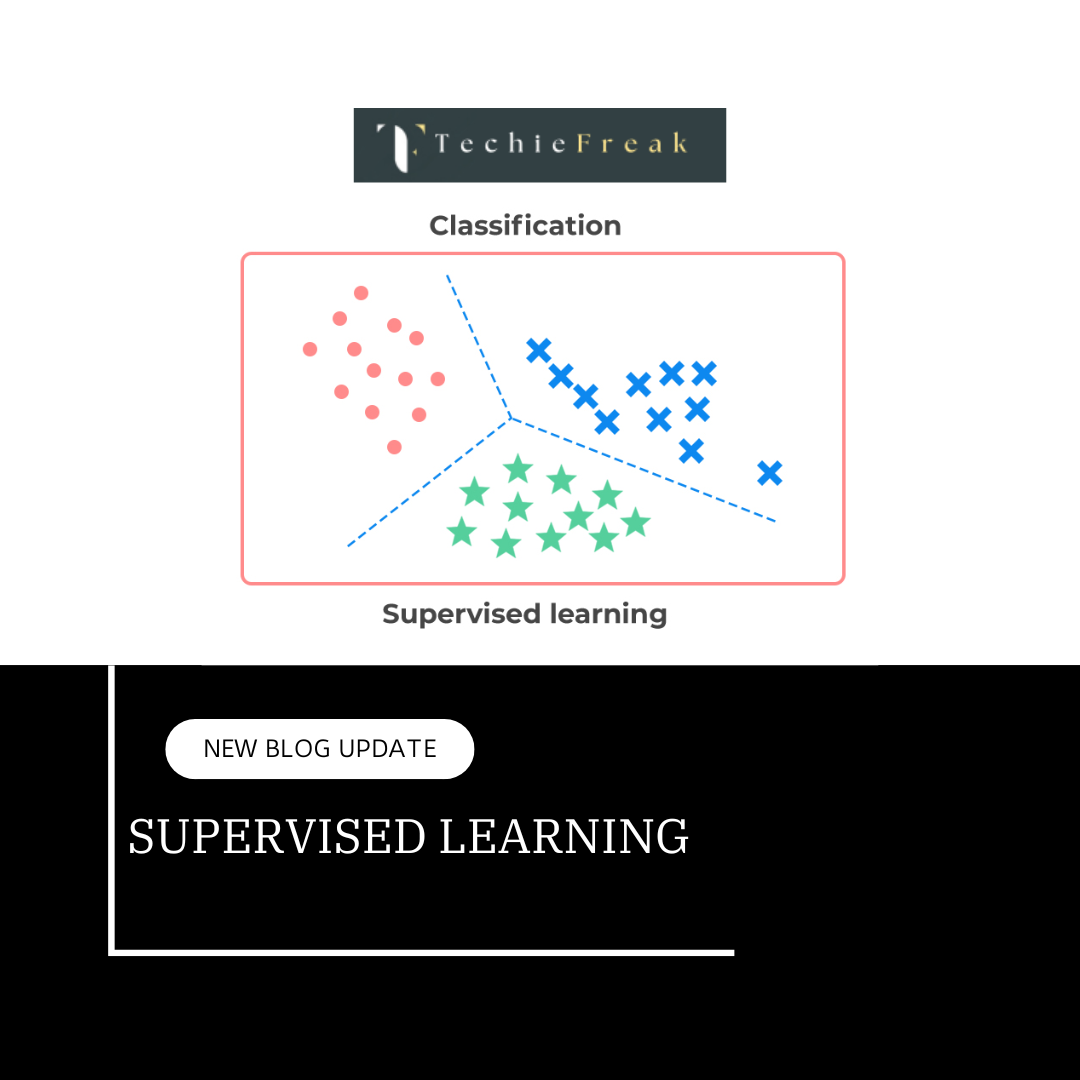
Bias-Variance Tradeoff in Lasso Regression

1. Bias in Lasso Regression

• Lasso Regression introduces bias by shrinking some coefficients toward zero or even setting them exactly to zero.
• This bias is introduced to reduce variance and prevent overfitting, especially when the dataset contains highly correlated features or when the number of features is large compared to the number of observations.
• As the regularization parameter (λ) increases, the model becomes more biased because the penalty forces the coefficients to shrink more aggressively.

2. Variance in Lasso Regression

• By reducing the magnitude of coefficients (or eliminating some of them altogether), Lasso reduces the model's complexity and, consequently, its variance.
• Lower variance means the model becomes less sensitive to noise in the training data, which improves its performance on unseen data (better generalization).

3. The Tradeoff

• High λ:
  • Strong regularization increases bias.
  • This results in underfitting because the model becomes too simplistic to capture the underlying relationships in the data.
• Low λ:
  • Weak regularization decreases bias but increases variance.
  • The model may overfit the training data, capturing noise instead of the true signal.
• The optimal λ balances this tradeoff by minimizing the total error (sum of bias squared, variance, and irreducible error).

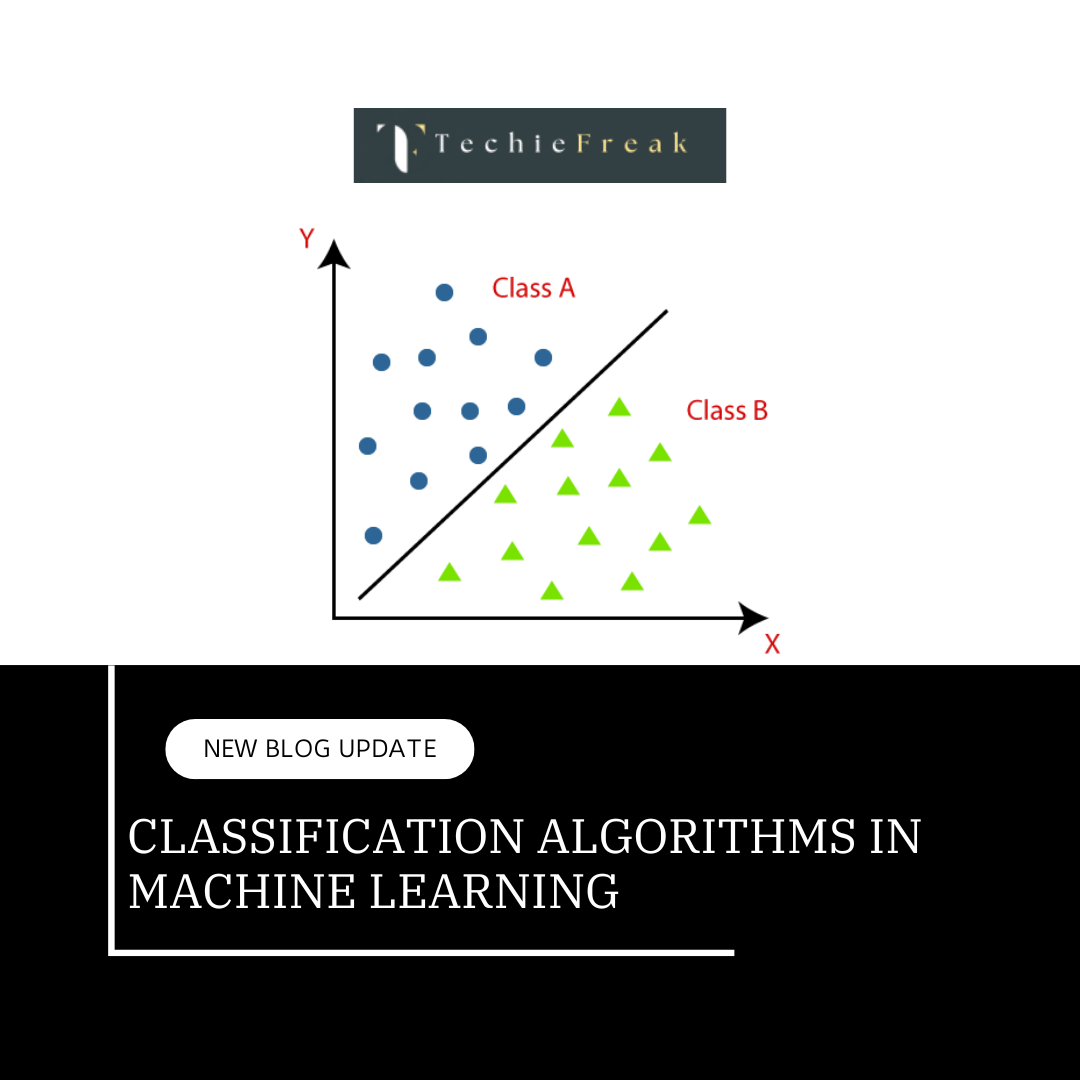
How Lasso Regression Works

Lasso Regression, short for Least Absolute Shrinkage and Selection Operator, is a linear regression technique that uses L1 regularization to prevent overfitting and enhance interpretability by shrinking some coefficients to exactly zero. This makes it particularly useful in datasets with many irrelevant or redundant features.

Step-by-Step Explanation

1. The Linear Regression Model

Lasso Regression starts with a basic linear regression model:

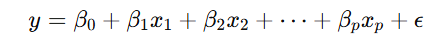
Where:

• y: Target variable
• x1,x2,…,xp: Predictor variables
• β0: Intercept
• β1,β2,…,βp: Coefficients of predictors
• ϵ: Error term

2. The Cost Function

In linear regression, the cost function is the Residual Sum of Squares (RSS):

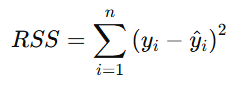
In Lasso Regression, an L1 regularization term is added to the RSS to penalize the absolute values of the coefficients:

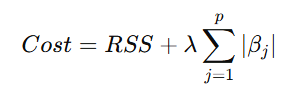
Where:

• λ: Regularization parameter that controls the strength of the penalty.
  • If λ=0, the model behaves like ordinary linear regression.
  • As λ increases, the penalty grows, shrinking the coefficients.

3. The Effect of the L1 Penalty

• The L1 penalty forces some coefficients (βj\beta_j) to exactly zero when λ\lambda is large enough. This effectively removes those features from the model, performing automatic feature selection.
• For features with smaller contributions to the target, the L1 penalty shrinks their coefficients more aggressively compared to features with larger contributions.

4. Optimization Process

The goal of Lasso Regression is to minimize the cost function:

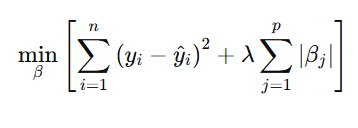
The optimization process:

1. Starts by initializing coefficients.
2. Iteratively updates the coefficients to minimize the combined error (RSS + penalty).
3. Applies soft-thresholding to shrink coefficients toward zero.

5. Regularization Path

As λ\lambda changes:

• For small λ: Minimal penalty, resulting in coefficients similar to those of linear regression.
• For large λ: Strong penalty, shrinking more coefficients to zero and creating a sparse model.

Why Lasso Regression is Powerful

1. Feature Selection: By shrinking some coefficients to zero, Lasso automatically identifies the most important features and eliminates irrelevant ones.
2. Handles Multicollinearity: Lasso works well when predictors are highly correlated by selecting one feature and shrinking the others.
3. Prevents Overfitting: The L1 penalty discourages overly complex models, improving generalization on unseen data.
4. Interpretability: Sparse models are easier to interpret, as only significant features are retained.

Comparison with Ridge Regression

• Lasso Regression: Uses L1 regularization and sets some coefficients to zero, leading to sparse solutions.
• Ridge Regression: Uses L2 regularization (penalty on the square of coefficients), shrinking coefficients but never exactly to zero.

Practical Implementation

In Python, Lasso Regression can be implemented using the Lasso class from the scikit-learn library:

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Split dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit the Lasso model
lasso = Lasso(alpha=0.1)  # alpha is the regularization parameter (\(\lambda\))
lasso.fit(X_train, y_train)

# Make predictions
y_pred = lasso.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

When to Use Lasso Regression

Lasso Regression is a powerful tool for regression analysis, but its effectiveness depends on the characteristics of your dataset and your goals. Below are scenarios where Lasso Regression is particularly useful:

1. When Feature Selection is Needed

• Lasso can automatically select important features by shrinking some coefficients to zero.
• Ideal for datasets with many irrelevant or redundant features.
• Example: In genetics, where thousands of gene expressions are used to predict a disease, Lasso helps identify the most relevant genes.

2. When the Dataset has High Dimensionality

• If the number of predictors (pp) is greater than or comparable to the number of observations (nn), Lasso is effective in avoiding overfitting.
• It is particularly useful in sparse data scenarios where only a subset of features truly influences the target variable.

3. When Multicollinearity is Present

• In cases of multicollinearity (high correlation between predictors), Lasso can select one of the correlated predictors and shrink the others to zero, reducing redundancy.
• This contrasts with Ridge Regression, which distributes the penalty across correlated features without setting any to zero.

4. When Model Interpretability is a Priority

• Lasso produces a sparse model by eliminating irrelevant features, making the model easier to interpret.
• Useful when you need a clear understanding of which predictors are contributing to the output.

5. To Prevent Overfitting

• The L1 penalty in Lasso limits the size of coefficients, which reduces the model’s complexity and helps avoid overfitting, especially when the data has noise.

6. When You Want a Balance Between Prediction and Feature Reduction

• Lasso can strike a balance between building a predictive model and identifying key features, making it suitable for applications where interpretability and accuracy are equally important.

7. When Computational Efficiency is Important

• For high-dimensional datasets, Lasso is computationally efficient because it reduces the number of active features, simplifying the optimization problem.

When NOT to Use Lasso Regression

1. When All Features are Important:

   • If every predictor contributes meaningfully to the outcome, Ridge Regression or Elastic Net might be better since Lasso may shrink some coefficients to zero unnecessarily.

2. When Multicollinearity is Severe and All Features are Important:

   • Ridge Regression is often preferred in such cases because it shrinks coefficients without eliminating any.

3. When the Dataset is Small or Low Dimensional:

   • In small datasets with low dimensionality, the bias introduced by Lasso may outweigh its benefits.

Alternatives to Consider

• Ridge Regression: If all features contribute and multicollinearity is an issue, use Ridge (L2 regularization).
• Elastic Net: Combines the strengths of Lasso and Ridge by balancing L1 and L2 penalties. Useful when both sparsity and multicollinearity are present.
• Feature Engineering: If feature selection is critical but automatic methods aren't sufficient, manual feature engineering might be necessary.

Practical Examples

1. Healthcare: Selecting biomarkers that predict a patient’s response to a treatment.
2. Finance: Identifying key factors influencing stock prices or credit risk.
3. Marketing: Determining which customer attributes (age, income, preferences) drive purchasing behavior.
4. Machine Learning Pipelines: As a preprocessing step to reduce the dimensionality of the feature set.

Advantages of Lasso Regression

• Feature Selection: Lasso regression eliminates the need to manually select the most relevant features, hence, the developed regression model becomes simpler and more explainable.
• Regularization: Lasso constrains large coefficients, so a less biased model is generated, which is robust and general in its predictions.
• Interpretability: With lasso, models are often sparsity induced, therefore, they are easier to interpret and explain, which is essential in fields like health care and finance.
• Handles Large Feature Spaces: Lasso lends itself to dealing with high-dimensional data like we have in genomic as well as imaging studies.

Disadvantages of Lasso Regression

• Selection Bias: Lasso, might arbitrarily choose one variable in a group of highly correlated variables rather than the other, thereby yielding a biased model in the end.
• Sensitive to Scale: Lasso is demanding in the respect that features of different orders have a tendency to affect the regularization line and the model's precision.
• Impact of Outliers: Lasso can be easily affected by the outliers in the given data, resulting into the overfitting of the coefficients.
• Model Instability: In the environment of multiple correlated variables the lasso's selection of variable may be unstable, which results in different variable subsets each time in tiny data change.
• Tuning Parameter Selection: Analyzing different λ (alpha) values may be problematic and maybe solved by cross-validation.

Next Topic- Python implementation of Lasso Regression