What is Logistic Regression?

Logistic regression is a supervised gadget gaining knowledge of set of rules used for class responsibilities wherein the intention is to expect the opportunity that an example belongs to a given magnificence or not. Logistic regression is a statistical set of rules which examine the connection among statistics factors. The article explores the basics of logistic regression, it`s kinds and implementations.

Logistic regression is used for binary class wherein we use sigmoid characteristic, that takes enter as unbiased variables and produces a opportunity fee among zero and 1.
For example, we've lessons Class zero and Class 1 if the fee of the logistic characteristic for an enter is more than zero.5 (threshold fee) then it belongs to Class 1 in any other case it belongs to Class zero. It`s called regression due to the fact it's miles the extension of linear regression however is specially used for class problems.

Key Points:
• Logistic regression predicts the output of a express structured variable. Therefore, the final results have to be a express or discrete fee.
• It may be both Yes or No, zero or 1, genuine or False, etc. however in preference to giving the precise fee as zero and 1, it offers the probabilistic values which lie among zero and 1.
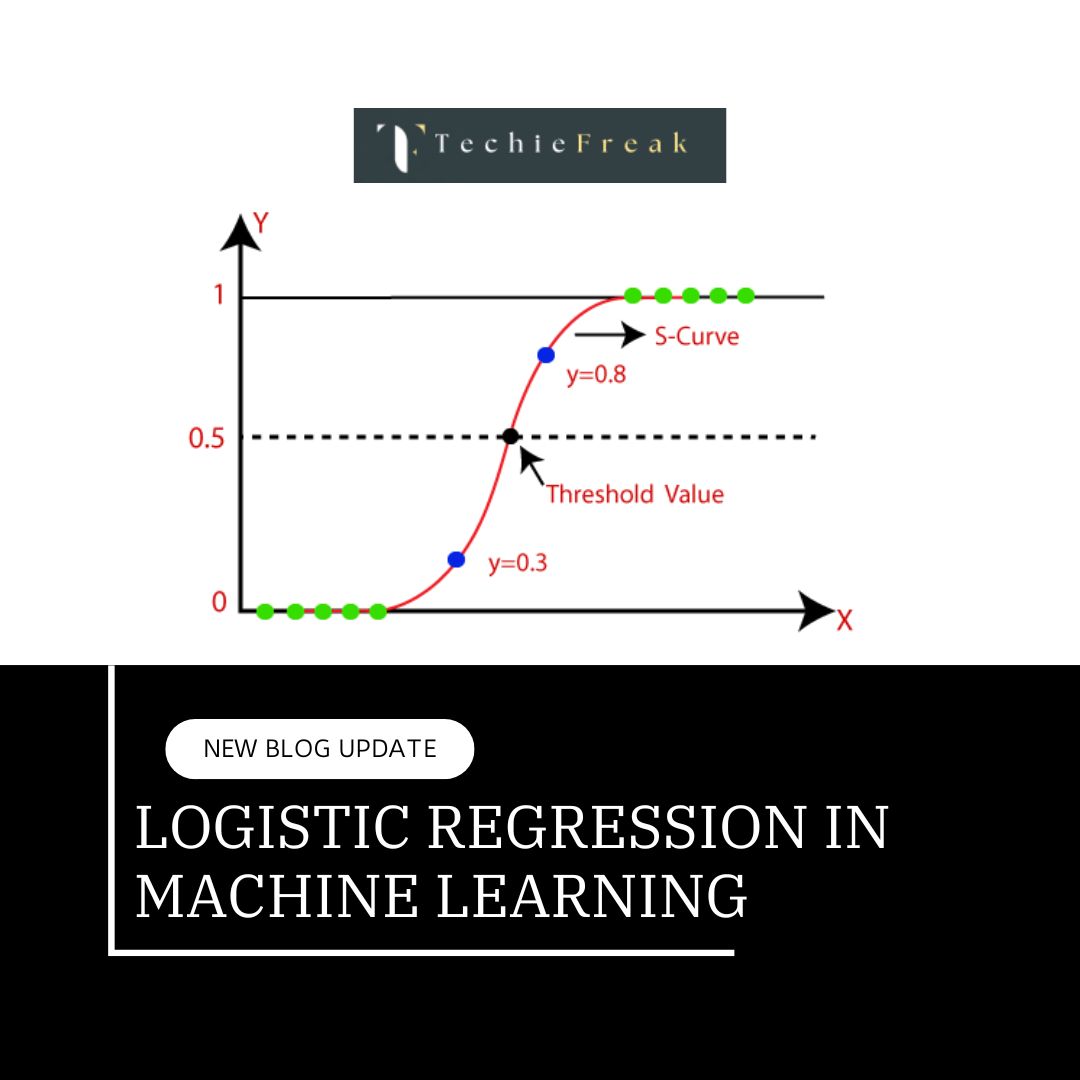
• In Logistic regression, in preference to becoming a regression line, we in shape an “S” shaped logistic characteristic, which predicts most values (zero or 1).

Logistic Function - Sigmoid Function
• Sigmoid function is a mathematical function that assigns a probability to a predicted value.
• It maps each real value to another value in the range of 0 to 1. Since the values ​​in logistic regression are between 0 and 1 and cannot go beyond this limit, they form an “S” shaped curve.
• The S shaped curve is called the sigmoid or logistic function.
• Logistic regression uses the concept of a threshold that defines the probability of 0 or 1. For example, values ​​above the threshold approach 1 and values ​​below the threshold approach 0.

Types of Logistic Regression
Based on the categories, logistic regression is divided into three types:
1. Binomial: In binomial logistic regression, there can be only two types of dependent variable. Ex: 0 or 1, pass or fail, etc.
2. Polynomial: In polynomial logistic regression, there can be three or more unordered types of dependent variable. Ex: “Cat”, “Dog”, “Sheep”
3. Ordinal: In ordinal logistic regression, there can be three or more ordered dependent variable types, such as "low", "medium", and "high".

Logistic Regression Assumptions
Understanding the assumptions of logistic regression is important to successfully apply the model, so let's review these assumptions. The assumptions include:
1. Independent Observations: Each observation is independent of other observations. This means that there is no correlation between the input variables.
2. Binary dependent variable: It is assumed that the dependent variable must be a binary or dichotomous variable. h. It can have only two values. For more than two categories, the SoftMax function is used.
3. Linear relationship between independent variable and log odds: The relationship between the independent variable and the log odds of the dependent variable must be linear.
4. No outliers: The dataset should not have any outliers.
5. Large sample: The sample is large enough.

Logistic Regression Terminology
Here are some common logistic regression terms:

• Independent variables: The input characteristics or predictors that are applied to predict the dependent variable.
• Dependent variable: The target variable in the logistic regression model that you are trying to predict.
• Logistic function: The equation used to describe how the independent and dependent variables relate to each other. The logistic function converts the input variables into a probability value between 0 and 1, which represents the probability that the dependent variable is 1 or 0.
• Odds: This is the ratio of something occurring to something not occurring. Probability differs from probability because it is the ratio of the chance of something happening to all the possible probabilities of it happening.
• Log odds: Log odds, also known as the logit function, is the natural logarithm of the odds. In logistic regression, the log odds of the dependent variable are modeled as a linear combination of the independent variables and an intercept.
• Coefficients: The estimated parameters in a logistic regression model indicate how the independent and dependent variables are related to each other.
• Intercept: The constant term in a logistic regression model, which represents the log odds when all the independent variables are zero.
• Maximum Likelihood Estimation: A method for estimating the coefficients of a logistic regression model that maximizes the probability of observing the data given the model.
 

How does Logistic Regression work?

The logistic regression model transforms the linear regression function continuous value output into categorical value output using a sigmoid function, which maps any real-valued set of independent variables input into a value between 0 and 1. This function is known as the logistic function.

Let the independent input features be:

and the dependent variable is Y having only binary value i.e. 0 or 1. 

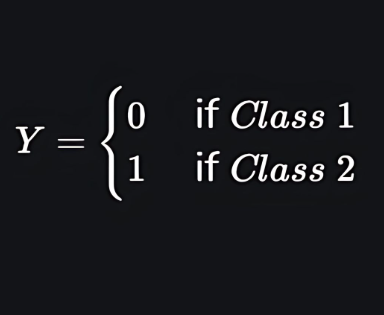
then, apply the multi-linear function to the input variables X.

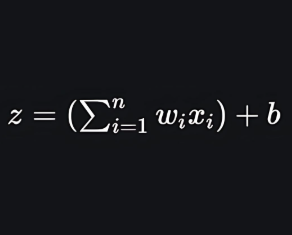
Here  x i x  i ​   is the ith observation of X,  w i = [ w 1 , w 2 , w 3 , ⋯ , w m ] w  i ​  =[w  1 ​  ,w  2 ​  ,w  3 ​  ,⋯,w  m ​  ] is the weights or Coefficient, and b is the bias term also known as intercept. simply this can be represented as the dot product of weight and bias.

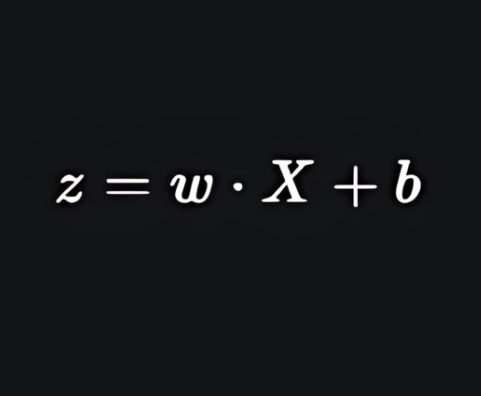
whatever we discussed above is the linear regression. 

Sigmoid Function

Now we use the sigmoid function where the input will be z and we find the probability between 0 and 1. i.e. predicted y.

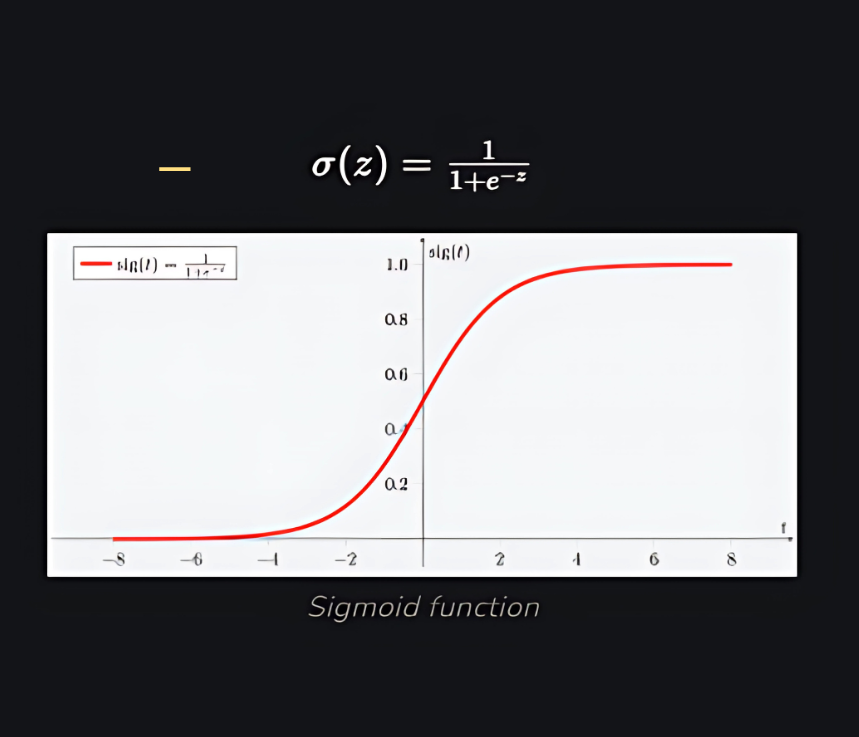
As shown above, the figure sigmoid function converts the continuous variable data into the probability i.e. between 0 and 1. 

• σ(z)   σ(z)  tends towards 1 as z→∞z→∞
• σ(z)   σ(z)  tends towards 0 as z→−∞z→−∞
• σ(z)   σ(z)  is always bounded between 0 and 1

where the probability of being a class can be measured as:

Logistic Regression Equation

The odd is the ratio of something occurring to something not occurring. it is different from probability as the probability is the ratio of something occurring to everything that could possibly occur. so odd will be:

Applying natural log on odd. then log odd will be:

then the final logistic regression equation will be:

Likelihood Function for Logistic Regression

The predicted probabilities will be:

• for y=1 The predicted probabilities will be: p(X;b,w) = p(x)

• for y = 0 The predicted probabilities will be: 1-p(X;b,w) = 1-p(x)

  

Taking natural logs on both sides

Gradient of the log-likelihood function

To find the maximum likelihood estimates, we differentiate w.r.t w,

How to Evaluate Logistic Regression Model?

Logistic regression is commonly used for binary classification tasks, and evaluating its performance is crucial to ensure accuracy and effectiveness. Below are key evaluation metrics and methods:

• Accuracy: 
  Accuracy provides the proportion of correctly classified instances.

  Use Accuracy When:

• The dataset is balanced (similar proportion of classes).
• Quick performance assessment is sufficient.

•  Confusion Matrix

  A confusion matrix summarizes the model's performance by categorizing predictions into:

• True Positive (TP): Correctly predicted positive outcomes.
• True Negative (TN): Correctly predicted negative outcomes.
• False Positive (FP): Incorrectly predicted positive outcomes.

• False Negative (FN): Incorrectly predicted negative outcomes.

  Use Confusion Matrix When:

• You want a detailed breakdown of prediction types.

• Evaluating imbalanced datasets.

   

• Precision: 
  Precision focuses on the accuracy of positive predictions

• Recall (Sensitivity or True Positive Rate): 
  Recall measures the proportion of correctly predicted positive instances among all actual positive instances.

  

• F1 Score: 
  F1 Score is the harmonic mean of precision and recall.

  

  Use Precision, Recall, and F1-Score When:

• The dataset is imbalanced.

• You need to balance false positives and false negatives based on business needs.
   

   ROC Curve and AUC (Area Under the Curve)

• ROC Curve: Plots True Positive Rate (TPR) vs. False Positive Rate (FPR) at different thresholds.

• AUC: Represents the area under the ROC curve. Higher AUC indicates better model performance.

  Use ROC-AUC When:

• You want to assess the model’s ability to distinguish between classes.

• You need threshold-independent evaluation.
   

   Log-Loss (Logarithmic Loss)

• Log-loss measures the model's uncertainty in making predictions. It calculates the likelihood of the predicted probabilities against the actual class.

  Use Log-Loss When:

• Probabilistic predictions (not just classifications) are required.

• Evaluating how confident the model is in its predictions.
   

  Cross-Validation

• Cross-validation splits the dataset into multiple subsets, training the model on one subset and testing it on the other. This helps avoid overfitting and ensures the model generalizes well.

  Use Cross-Validation When:

• You need a robust estimate of model performance.
• Dataset size is small or prone to overfitting.
   

• When to Use What?

  Scenario	Metric to Use
  Balanced Dataset	Accuracy, Precision, Recall, F1-Score
  Imbalanced Dataset	Precision, Recall, F1-Score, ROC-AUC
  Focus on Minimizing False Positives	Precision
  Focus on Minimizing False Negatives	Recall
  General Model Performance	Confusion Matrix, Accuracy
  Threshold-Independent Evaluation	ROC-AUC
  Confidence in Predictions	Log-Loss
  Small or Overfitting-Prone Dataset	Cross-Validation

  Key Takeaways :

• Definition: Logistic regression is a supervised machine learning algorithm used for classification tasks, predicting probabilities between 0 and 1.
• Sigmoid Function: The logistic regression model uses the sigmoid function to map input values to probabilities, forming an "S"-shaped curve.
• Types:
  • Binomial: Two categories (e.g., 0 or 1).
  • Multinomial: Multiple unordered categories (e.g., Cat, Dog).
  • Ordinal: Multiple ordered categories (e.g., Low, Medium, High).
• Assumptions: Includes independent observations, binary dependent variables, linear relationships (log odds), no outliers, and large datasets.
• Evaluation Metrics:
  • Accuracy, Precision, Recall, F1-Score: Assess model performance.
  • ROC-AUC: Threshold-independent evaluation.
  • Confusion Matrix: Breakdown of prediction types.
  • Log-Loss: Evaluates confidence in probabilistic predictions.
• Applications: Logistic regression is widely used in classification tasks such as spam detection, disease prediction, and risk assessment.

• When to Use Metrics:

  • Balanced datasets: Accuracy, F1-Score.
  • Imbalanced datasets: Precision, Recall, ROC-AUC.

  
  Next Blog-  Python Implementation of Logistic Regression