K-Nearest Neighbor (KNN) Algorithm
K-Nearest Neighbors (KNN) is one of the simplest yet powerful machine learning algorithms used for both classification and regression tasks. Despite being intuitive, KNN can often produce strong performance in predictive modeling, especially when the data is easy to interpret and non-linear. In this blog, we'll explore the KNN algorithm, its working mechanism, advantages, limitations, and an example to demonstrate how it works.
Why do we need the K-NN algorithm?
- K-NN (K-Nearest Neighbor) is a simple and intuitive algorithm primarily used for classification and regression tasks
- It makes no assumptions about the distribution of the data (non-parametric).
- It is useful when predictions need to be made based on the similarity between data points.
Applications: Spam detection, pattern recognition, recommendation systems.

How KNN Algorithm Works
The working of KNN can be explained in a few simple steps.
Steps of KNN Algorithm:
- Step 1: Choose the value of K
Select the number of nearest neighbors (K) you want to consider for making a prediction. - Step 2: Calculate Distance Between Data Points
Compute the distance between the new data point (test point) and all points in the training dataset. Common distance metrics are Euclidean, Manhattan, and Minkowski distance. - Step 3: Identify K Nearest Neighbors
Sort the distances in ascending order and select the K smallest distances. These K data points are the nearest neighbors. - Step 4: Make Predictions
- For Classification: The class label is determined by the majority class among the K nearest neighbors.
- For Regression: The predicted value is the average (or weighted average) of the values of the K nearest neighbors.
- Step 5: Return the Result
Return the predicted class label or value as the output.
What Are Hyperparameters?
Hyperparameters are configuration parameters set before training a machine learning model. Unlike model parameters (which are learned during training), hyperparameters are externally defined to control how the learning process operates.
For example:
- In KNN, the "K value" (number of neighbors) is a hyperparameter.
- In neural networks, the "learning rate" or "number of layers" are hyperparameters.
Key Hyperparameters in KNN
There are a few important hyperparameters that affect the performance of the KNN algorithm. Let’s look at the most significant ones.
K Value
The K value (number of neighbors) is one of the most critical parameters in KNN. A small K value makes the model sensitive to noise, while a larger K value might smooth out the predictions too much. The choice of K can significantly impact the accuracy and performance of the algorithm.
- Small K: More sensitive to noise.
- Large K: Can smooth out predictions but might miss finer details in the data.
Distance Metrics
Distance metrics define how the distance between data points is measured. The most commonly used distance metric is Euclidean distance, but there are others, like Manhattan and Minkowski distance.
Weights
In some cases, you might not want each neighbor to contribute equally to the prediction. The weights parameter allows you to assign different weights to neighbors based on their distance from the test point. Closer neighbors can have higher weights, influencing the prediction more than farther neighbors.
Why Are Hyperparameters Important?
Hyperparameters significantly impact a model's performance and efficiency. Here's why:
- Model Performance: Correctly tuned hyperparameters improve accuracy and generalization to unseen data.
- Example: In KNN, choosing the right K value prevents overfitting or underfitting.
- Training Efficiency: Optimal hyperparameters reduce training time and computational resources.
- Avoid Overfitting/Underfitting: Hyperparameters like regularization terms or dropout rates help balance the model's ability to generalize and adapt to new data.
- Model Customization: Different hyperparameters can adapt a model to specific datasets and tasks (e.g., binary vs. multiclass classificatio
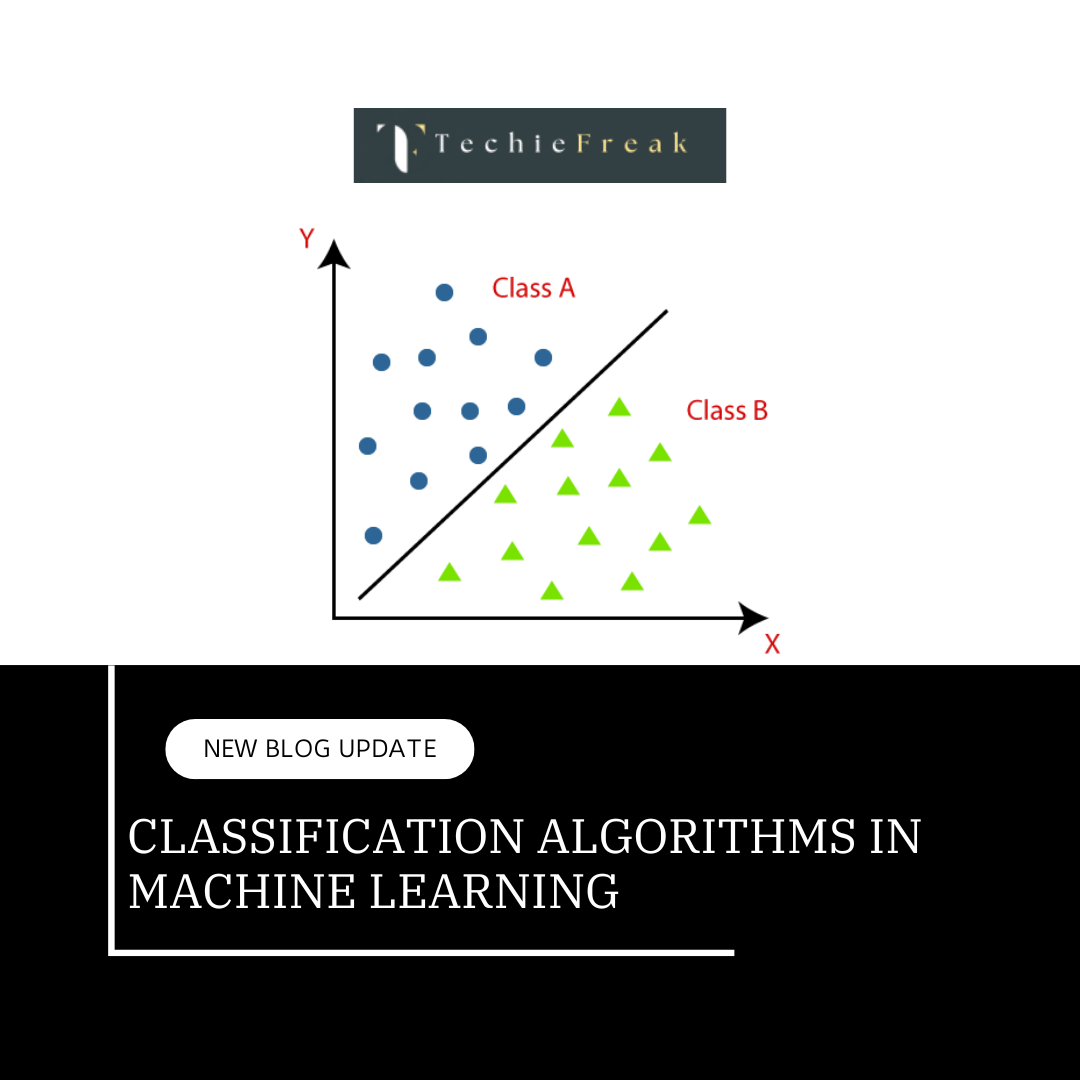
Types of Problems KNN Solves
KNN can solve both classification and regression problems.
Classification Problem
In classification tasks, the algorithm assigns the majority class label from the K nearest neighbors. For example, if you want to classify an animal, the algorithm looks at the K nearest animals (based on features like size, weight, etc.) and assigns the class that appears the most.
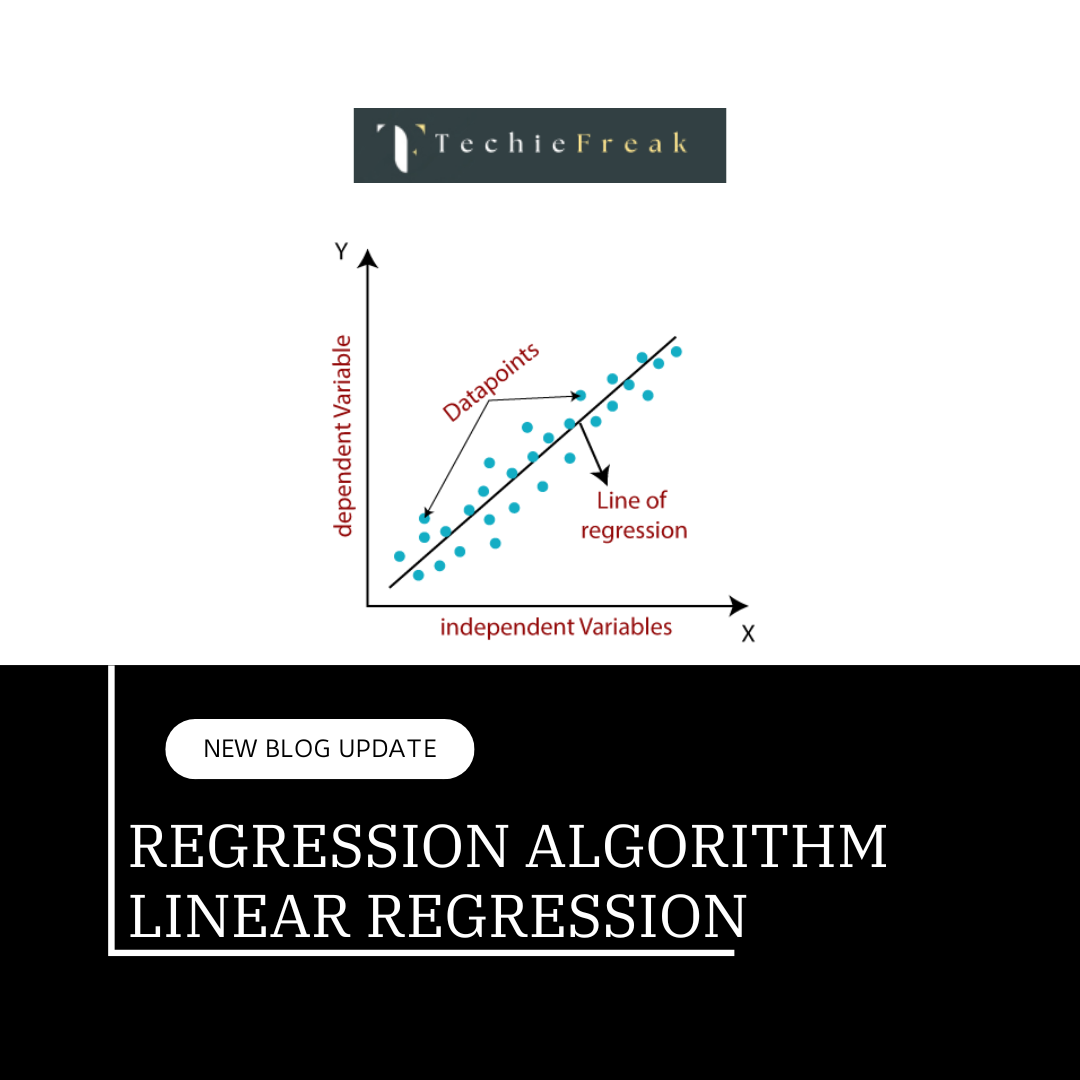
Regression Problem
In regression tasks, KNN assigns a predicted value based on the average (or weighted average) of the values of the K nearest neighbors. For example, predicting the price of a house based on similar houses' prices.
KNN Distance Metrics
Distance metrics are crucial in KNN because they help in finding the similarity between data points. Below are the most commonly used distance metrics.
Euclidean Distance
The Euclidean distance is the straight-line distance between two points in the feature space. It is the most commonly used metric.
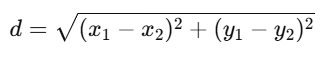
Manhattan Distance
The Manhattan distance calculates the distance between points by summing the absolute differences of their coordinates.
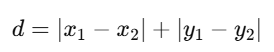
Minkowski Distance
The Minkowski distance generalizes both Euclidean and Manhattan distances. It introduces a parameter p to control the distance computation.
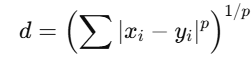
KNN Algorithm – Example
Let’s consider an example to illustrate how KNN works.
Example: Classifying Animals Based on Weight and Height
We have a dataset of animals with their respective height and weight as features and animal type as labels (e.g., "Dog", "Cat", "Horse").
Training Dataset:
| Animal Type | Height (cm) | Weight (kg) |
|---|---|---|
| Dog | 40 | 12 |
| Dog | 50 | 15 |
| Cat | 30 | 4 |
| Cat | 35 | 5 |
| Horse | 150 | 500 |
Test Point: We want to classify a new animal with a height of 38 cm and a weight of 10 kg.
- Calculate Distance: Use Euclidean distance to calculate the distance from the test point to each point in the training dataset.
- Find K Nearest Neighbors: Let’s choose K=3. The three closest animals are selected based on the smallest distances.
- Make Prediction: Since 2 of the 3 nearest neighbors are labeled "Dog", the test point is classified as "Dog".
How to Select the Value of K:
- A small K captures finer patterns but risks overfitting.
- A large K smooths the model but risks underfitting.
- Optimal K: Use cross-validation to test multiple KKK values.
- Rule of thumb: K≈NK \approx \sqrt{N}K≈N, where NNN is the total number of data points.
Advantages of K-NN:
- Simplicity: Easy to put in force and intuitive.
- Versatile: Works for class and regression.
- Non-parametric: Makes no assumptions approximately information distribution.
Disadvantages of K-NN:
- Computationally Expensive: Slow for massive datasets because of distance calculations.
- Sensitive to Irrelevant Features: Performance degrades with out characteristic scaling.
- Curse of Dimensionality: Effectiveness reduces with growing dimensions.
When to Use KNN
- Small Datasets: KNN is ideal for small to medium-sized datasets. For large datasets, the computational complexity increases.
- Low-Feature Space: KNN works well when the data points have fewer features (dimensions). In high-dimensional spaces, the performance may degrade due to the curse of dimensionality.
- Real-time Applications: If predictions need to be made quickly and the model doesn’t require training, KNN is a good option.
Key Takeaways-
- What is KNN?
- A simple, non-parametric machine learning algorithm for classification and regression tasks.
- Based on similarity between data points.
- How KNN Works:
- Step 1: Choose the number of neighbors (K).
- Step 2: Calculate distance (e.g., Euclidean, Manhattan).
- Step 3: Identify K nearest neighbors.
- Step 4: Make predictions (majority class for classification, average value for regression).
- Hyperparameters in KNN:
- K Value: Determines the number of neighbors.
- Small K → Sensitive to noise (overfitting).
- Large K → May miss finer details (underfitting).
- Distance Metrics: Euclidean, Manhattan, Minkowski.
- Weights: Assign higher weight to closer neighbors for better predictions.
- K Value: Determines the number of neighbors.
- Key Strengths:
- Simplicity: Intuitive and easy to implement.
- Versatility: Works for classification and regression.
- Non-parametric: No assumptions about data distribution.
- Limitations:
- Computationally expensive for large datasets.
- Sensitive to irrelevant features and requires feature scaling.
- Struggles with high-dimensional data (curse of dimensionality).
- Applications:
- Spam detection, recommendation systems, pattern recognition.
- Optimal K Selection:
- Use cross-validation or the rule of thumb K≈NK \approx \sqrt{N}K≈N (where NNN is the dataset size).
- When to Use KNN:
- Small to medium datasets with low feature dimensions.
- Real-time predictions where training isn’t needed.
 Algorithm for Machine Learning.jpg)

.png)
.png)
.png)

.png)
.png)
.png)
 Algorithm.jpg)

.png)
.png)
.png)
.png)
.png)
.png)
