Introduction to Neural Networks in Deep Learning
1. Understanding Neural Networks
Neural networks are the foundation of deep learning, a subset of machine learning that focuses on training models to recognize patterns and make decisions. Inspired by the human brain, neural networks consist of interconnected nodes, known as artificial neurons, that process and transmit information. These networks are capable of learning from data and improving their performance over time, making them a fundamental component in modern artificial intelligence applications.
Neural networks are widely used in tasks such as image and speech recognition, natural language processing, and decision-making systems. Their ability to learn complex patterns and relationships in data allows them to perform tasks that traditional algorithms struggle to handle.
2. Structure and Components of a Neural Network
A neural network consists of multiple layers of neurons that transform input data into meaningful outputs. These layers include:
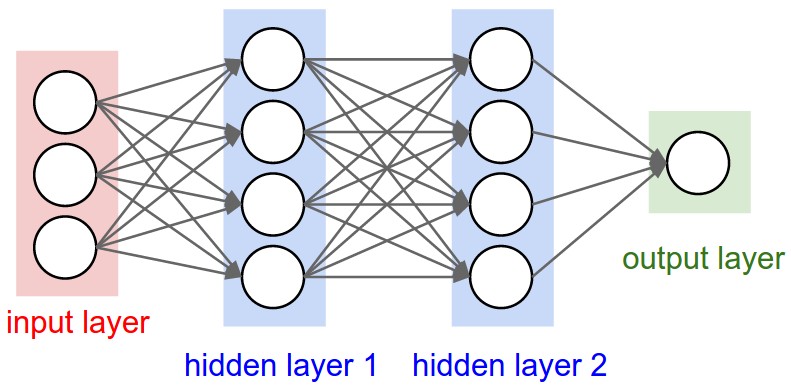
2.1 Input Layer
The input layer is the first layer in a neural network, responsible for receiving raw data before any processing occurs. Each neuron in the input layer represents a feature of the dataset.
Key Characteristics of the Input Layer:
- No computations occur in this layer; it only passes data forward.
- The number of neurons in the input layer depends on the number of input features.
- In image processing, each pixel in an image corresponds to an input neuron.
- In text processing, words or characters may be represented as numerical vectors.
Example of an Input Layer:
- For a grayscale image of size 28x28 pixels, the input layer has 784 neurons (since 28 × 28 = 784).
- For structured data with 10 numerical features, the input layer has 10 neurons.
2.2 Hidden Layers
Hidden layers are where most of the computations and learning take place in a neural network. Each neuron in a hidden layer receives inputs, applies a transformation, and passes the result to the next layer.
Key Characteristics of Hidden Layers:
- Extract features and patterns from the input data.
- Each neuron applies a mathematical transformation to the input data.
- The depth of a neural network is determined by the number of hidden layers.
- Deep networks (multiple hidden layers) can learn more complex and abstract features.
Operations in a Hidden Layer:
Each neuron in the hidden layer follows this equation:
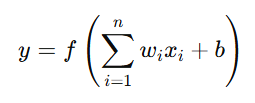
Where:
- y is the neuron's output.
- xi are the input values.
- wi are the weights assigned to each input.
- b is the bias term (adjusts the output independently of inputs).
- f is the activation function that introduces non-linearity.
Importance of Hidden Layers:
- Feature Extraction – Detects meaningful patterns (e.g., edges in images).
- Non-linearity – Allows learning of complex relationships.
- Representation Learning – Deep networks automatically discover hierarchical representations of data.
Example of Hidden Layers in Action:
- In image classification, early hidden layers detect simple patterns (edges, colors), while deeper layers detect complex objects (faces, animals).
- In speech recognition, hidden layers capture frequency variations and linguistic features.
2.3 Output Layer
The output layer provides the final prediction or decision of the neural network. The number of neurons in the output layer depends on the problem type:
Types of Output Layers:
- Classification Tasks
- The output layer contains one neuron per class.
- Example: In a digit recognition task (0-9), the output layer has 10 neurons, each representing a digit.
- The softmax activation function is commonly used to output probabilities for each class.
- Binary Classification
- The output layer has one neuron with a sigmoid activation function.
- Example: In spam detection, the network predicts either spam (1) or not spam (0).
- Regression Tasks
- The output layer has one neuron that provides a continuous numeric value.
- The linear activation function is commonly used.
- Example: Predicting house prices based on input features.
Example of an Output Layer:
- Image Classification (Dog vs. Cat):
- 2 neurons in the output layer (one for "Dog", one for "Cat").
- Uses Softmax activation to output probabilities.
- Stock Price Prediction:
- 1 neuron in the output layer for predicting a continuous value.
- Uses a Linear activation function.
2.4 Neurons and Connections
Each neuron in a neural network is a small computational unit that processes inputs and passes outputs to the next layer. It is modeled mathematically using weights, biases, and activation functions.
Neuron Computation Process:
Each neuron performs the following computation:
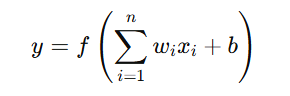
Where:
- xi = Inputs to the neuron.
- wi = Weights assigned to each input.
- b = Bias term.
- f = Activation function.
- y = Output of the neuron.
1. Weights (wi)
- Weights determine the importance of each input.
- Higher weights indicate a stronger influence on the output.
- Weights are learned during training using gradient descent.
2. Bias (b)
- The bias allows the activation function to shift up or down.
- Bias ensures the network learns patterns that don’t pass through the origin.
3. Activation Function (f)
- The activation function introduces non-linearity, enabling the network to learn complex relationships.
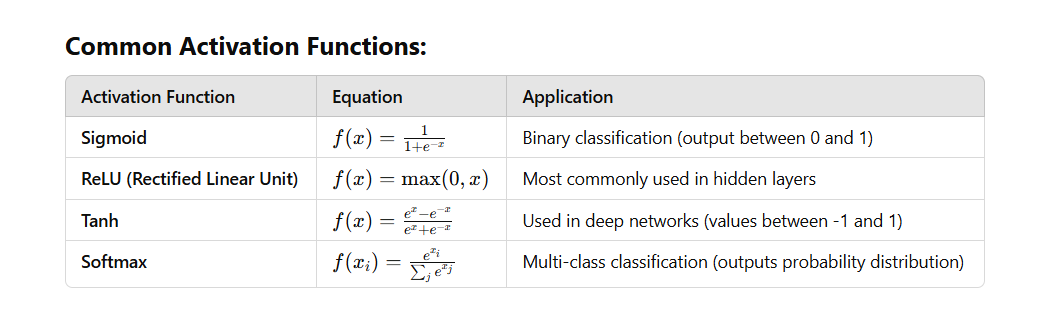
3. Activation Functions
Activation functions play a crucial role in neural networks by introducing non-linearity into the model. Without activation functions, a neural network would behave like a simple linear regression model, regardless of its depth. Activation functions determine whether a neuron should be activated based on its input, enabling the network to learn complex patterns and make accurate predictions.
There are different types of activation functions, each with its own advantages and disadvantages. Below are some of the most commonly used ones:
3.1 Sigmoid Function
The sigmoid activation function maps input values into a range between 0 and 1, making it useful for binary classification tasks. It is defined as:
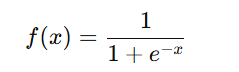
Properties of the Sigmoid Function:
- Range: (0,1)
- Shape: S-shaped curve (also called the logistic function)
- Interpretability: Since the output is between 0 and 1, it can be interpreted as a probability, making it useful for logistic regression and binary classification tasks.
Disadvantages:
- Vanishing Gradient Problem:
- In deep networks, the gradients of weights in earlier layers become very small (almost zero) when using backpropagation. This slows down training and makes it difficult to update the weights effectively.
- Not Zero-Centered:
- The function always produces positive values, which can lead to inefficient weight updates during optimization.
- Computationally Expensive:
- Since the function involves exponentiation, it is computationally expensive compared to simpler functions like ReLU.
Use Cases:
- Logistic regression
- Output layer in binary classification problems
3.2 ReLU (Rectified Linear Unit)
The Rectified Linear Unit (ReLU) is the most commonly used activation function in deep learning because of its simplicity and effectiveness. It is defined as:
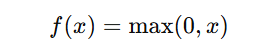
This means:
- If x>0, then f(x)=x
- If x≤0, then f(x)=0
Properties of ReLU:
- Range: (0, ∞)
- Non-linear: Introduces non-linearity, allowing deep networks to learn complex patterns.
- Efficient Computation: Simple mathematical operations (max operation) make it computationally efficient.
Advantages:
- Solves the Vanishing Gradient Problem:
- Unlike sigmoid and tanh, ReLU does not saturate in the positive region, allowing better gradient propagation and faster training.
- Sparse Activation:
- If the input is negative, the output is zero. This leads to sparsity in the network, making it more efficient.
- Computationally Efficient:
- Only requires a comparison operation, which is much faster than exponentiation.
Disadvantages:
- Dying ReLU Problem:
- If a neuron's input is always negative, it will always output zero, meaning the neuron becomes inactive and stops learning.
- A possible solution is Leaky ReLU, which allows small negative values instead of zero.
Use Cases:
- Hidden layers in deep learning models
- CNNs (Convolutional Neural Networks)
- Large-scale deep learning models due to its efficiency
3.3 Softmax Function
The softmax activation function is primarily used in the output layer of multi-class classification problems. It converts raw scores (logits) into probabilities that sum up to 1. It is defined as:
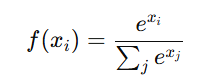
Where:
- xi is the input to the function (logits)
- exi exponentiates the input
- The denominator ensures that the sum of all outputs is 1
Properties of Softmax:
- Outputs Probabilities: Converts raw scores into probability distributions.
- Ensures Sum of Outputs = 1: This makes it useful for classification tasks.
- Enhances Model Interpretability: The output values can be directly interpreted as probabilities for each class.
Advantages:
- Probabilistic Interpretation:
- Outputs can be directly interpreted as class probabilities, making it useful in classification tasks.
- Ensures Differentiability:
- Helps in smooth gradient updates during backpropagation.
Disadvantages:
- Can be Sensitive to Large Logits:
- If one value in the input vector is much larger than others, the function will push its probability close to 1, making other values close to 0.
- Computational Cost:
- Involves exponentiation and summation over all inputs, which can be computationally expensive in large-scale models.
Use Cases:
- Multi-class classification tasks (e.g., image classification using CNNs)
- NLP tasks (e.g., text classification)
| Activation Function | Suitable For | Advantages | Disadvantages |
|---|---|---|---|
| Sigmoid | Binary classification | Outputs probabilities | Vanishing gradient problem, computationally expensive |
| ReLU | Hidden layers in deep networks | Efficient, solves vanishing gradient issue | Dying ReLU problem |
| Softmax | Multi-class classification | Outputs probabilities that sum to 1 | Computationally expensive, sensitive to large values |
Each function has its own strengths and weaknesses, and deep learning models often combine different activation functions in different layers to optimize performance.
4. Training a Neural Network
Training a neural network is the process of adjusting its weights and biases so that it can make accurate predictions on unseen data. This process is iterative and involves multiple steps, including forward propagation, loss computation, backpropagation, and optimization. The goal is to minimize the error in predictions by updating the network’s parameters through gradient-based optimization techniques.
4.1 Forward Propagation
Forward propagation is the first step in training, where input data passes through the network layer by layer until it reaches the output layer. Each neuron processes the inputs using its weights, applies an activation function, and sends the result to the next layer.
Step-by-Step Process of Forward Propagation:
- Input Layer:
- The input layer receives the raw data, where each neuron corresponds to a feature of the dataset.
- Example: In an image, each pixel value is an input neuron.
- Hidden Layers:
- Each neuron in a hidden layer takes the weighted sum of inputs from the previous layer, adds a bias term, and applies an activation function to introduce non-linearity.
Mathematically, for a given neuron:
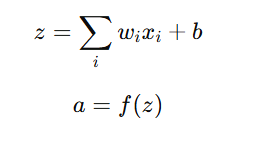
where:
- wi are the weights
- xi are the input values
- b is the bias
- f is the activation function
- z is the weighted sum
- a is the activated output
- Output Layer:
- The final layer processes the last set of weighted inputs and produces the predicted output.
- For classification tasks, a softmax or sigmoid function is applied to obtain probability values.
- For regression tasks, the output is a continuous numerical value.
4.2 Loss Function
A loss function measures how far the predicted output is from the actual output (ground truth). The lower the loss, the better the model’s performance. The choice of the loss function depends on the type of problem:
Common Loss Functions:
1. Mean Squared Error (MSE) – Used for Regression
MSE is used for predicting continuous values, where the difference between the actual and predicted value is squared to penalize large errors. It is calculated as:
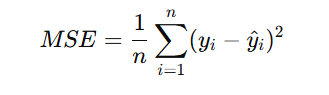
where:
- yi = actual value
- y^i = predicted value
- n = total number of samples
Why Use MSE?
- Penalizes large errors more than small ones (due to squaring).
- Differentiable, allowing for gradient-based optimization.
2. Mean Absolute Error (MAE) – Used for Regression
MAE calculates the average absolute differences between actual and predicted values:
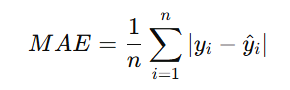

3. Cross-Entropy Loss – Used for Classification
Cross-entropy measures the difference between the actual and predicted probability distributions. It is commonly used for binary and multi-class classification:
Binary Cross-Entropy (Log Loss)
For binary classification:
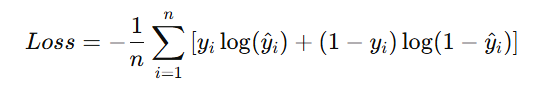
Categorical Cross-Entropy
For multi-class classification:
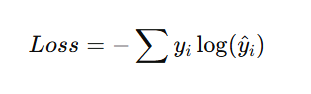
where:
- yi = actual class label (one-hot encoded)
- y^i = predicted probability of that class
4.3 Backpropagation and Optimization
Once the loss is calculated, the network needs to update its weights to minimize the error. This is done through backpropagation and optimization algorithms.
Backpropagation
Backpropagation is an algorithm used to compute the gradients of the loss function with respect to each weight in the network. It consists of:
- Computing the loss gradient with respect to the output.
- Propagating the error backwards through the layers using the chain rule of calculus.
- Updating the weights based on these gradients using an optimization algorithm.
Gradient Descent (Optimization Algorithm)
Gradient Descent is used to update weights in the direction that minimizes the loss function. The update rule is:
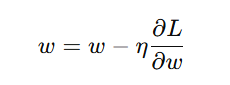
where:
- w = weight
- η = learning rate (controls step size)
- ∂L/∂w = gradient of loss with respect to weight
Types of Gradient Descent:
| Method | Description | Pros | Cons |
|---|---|---|---|
| Batch Gradient Descent | Uses all training data to update weights | Stable convergence | Slow for large datasets |
| Stochastic Gradient Descent (SGD) | Updates weights for each sample | Faster updates | High variance, noisy convergence |
| Mini-Batch Gradient Descent | Uses small batches of data to update weights | Balance between stability and speed | Needs tuning of batch size |
Adaptive Optimization Algorithms
More advanced optimizers modify the learning rate dynamically:
1. Momentum-Based Updates
Momentum is a technique used to accelerate gradient descent by smoothing updates and avoiding sudden changes in direction. Instead of updating weights solely based on the current gradient, momentum accumulates a moving average of past gradients, which helps the model converge faster and escape local minima.
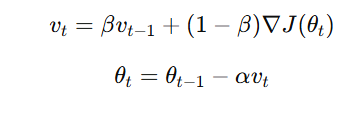
Formula for Momentum Update:
where:- vt is the velocity term (moving average of gradients).
- β (typically 0.9) is the momentum decay factor.
- ∇J(θt)) is the gradient of the loss function.
- α is the learning rate.
- θt represents model parameters.
Momentum helps in:
- Smoother updates: Reduces oscillations and prevents sharp changes in weight updates.
- Faster convergence: Accumulates previous gradients to keep moving in a preferred direction.
- Better handling of local minima: Helps escape shallow local minima by building velocity.
2. Adaptive Learning Rates
Adaptive learning rate methods adjust the learning rate for each parameter individually, ensuring efficient learning while preventing large, unstable updates.
Adam’s Adaptive Learning Rate Mechanism:
Adam (Adaptive Moment Estimation) keeps track of:- First moment estimate (mt): Moving average of gradients (momentum).
- Second moment estimate (vt): Moving average of squared gradients (variance).
The adaptive update rule is:
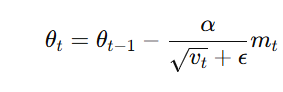
where:
- vt normalizes the step size based on gradient magnitudes.
- ϵ (small constant) prevents division by zero.
Benefits of Adaptive Learning Rates:
- Faster convergence by adjusting step sizes dynamically.
- Stability in noisy or non-stationary environments.
- Effective learning across different parameters since each weight has a different learning rate.
RMSprop (Root Mean Square Propagation) – Explained
RMSprop is an adaptive learning rate optimization algorithm that helps improve training stability and convergence speed, especially in deep learning models. It builds on ideas from AdaGrad but improves upon it by addressing its main weakness—rapidly decreasing learning rates.
How RMSprop Works
RMSprop normalizes the learning rate of each parameter by dividing it by the square root of a moving average of its recent squared gradients. This prevents large fluctuations in parameter updates and makes training smoother.
Mathematical Formulation
The update rule for RMSprop is:
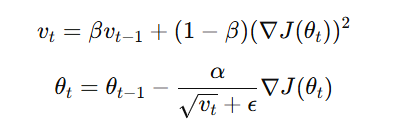
where:
- vt is the moving average of squared gradients (acts as normalization).
- β (typically 0.9) is the decay factor that controls how much past gradients influence the current step.
- ∇J(θt) is the gradient of the loss function with respect to the parameters.
- α is the learning rate.
- ϵ (small constant, usually 10−810^{-8}) prevents division by zero.
- θt represents the model parameters being updated.
Why RMSprop Helps?
- Prevents Oscillations:
- In standard gradient descent, the learning rate remains constant, which can lead to oscillations when gradients are large.
- RMSprop adapts learning rates based on recent gradient history, reducing fluctuations and making convergence smoother.
- Handles Non-Stationary Problems:
- Since it dynamically adjusts learning rates per parameter, it works well even when gradients change frequently.
- Balances Convergence Speed & Stability:
- Unlike AdaGrad, which aggressively reduces the learning rate over time, RMSprop maintains a more stable learning rate, ensuring efficient long-term training.
| Step | Purpose | Key Techniques |
|---|---|---|
| Forward Propagation | Computes output | Weighted sum, activation functions |
| Loss Calculation | Measures prediction error | MSE, Cross-Entropy |
| Backpropagation | Computes gradients | Chain rule, partial derivatives |
| Optimization | Updates weights | Gradient Descent, Adam, RMSprop |
5. Types of Neural Networks
Neural networks come in different architectures, each designed to handle specific types of data and tasks. Below is a detailed explanation of the most common types of neural networks:
5.1 Feedforward Neural Networks (FNNs)
Feedforward Neural Networks (FNNs) are the most basic type of artificial neural networks. The information flows in one direction—from the input layer, through hidden layers (if any), to the output layer.
Key Features:
- No loops or cycles in the network structure.
- Used for supervised learning tasks like classification and regression.
- Commonly trained using backpropagation and gradient descent.
Applications:
- Image and text classification
- Function approximation
- Medical diagnosis
5.2 Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) are specifically designed to process grid-like data, such as images and videos. They use convolutional layers to extract important spatial features like edges, textures, and patterns.
Key Features:
- Uses convolutional layers to apply filters (kernels) that detect patterns.
- Contains pooling layers to reduce the dimensionality of the data while preserving key features.
- Often includes fully connected layers for classification.
Applications:
- Image recognition (e.g., identifying objects in pictures)
- Facial recognition (e.g., unlocking phones using Face ID)
- Medical imaging (e.g., detecting tumors in X-rays)
5.3 Recurrent Neural Networks (RNNs)
Recurrent Neural Networks (RNNs) are designed to handle sequential data, where previous inputs influence the current output. Unlike FNNs, RNNs have feedback loops, allowing them to remember past information.
Key Features:
- Maintains hidden states to retain memory of previous inputs.
- Uses loop connections to process sequences like text, speech, and time-series data.
- Faces challenges like the vanishing gradient problem, making it difficult to learn long-term dependencies.
Applications:
- Speech recognition (e.g., Siri, Google Assistant)
- Language modeling (e.g., predictive text, chatbots)
- Time-series forecasting (e.g., stock price prediction)
5.4 Long Short-Term Memory Networks (LSTMs)
LSTMs are a type of RNN designed to overcome the vanishing gradient problem by introducing gates that regulate information flow.
Key Features:
- Uses forget, input, and output gates to control memory.
- Maintains long-term dependencies, unlike standard RNNs.
- Effective for tasks that require remembering long sequences.
Applications:
- Machine translation (e.g., Google Translate)
- Speech-to-text conversion (e.g., automatic captions)
- Financial forecasting (e.g., predicting stock trends)
5.5 Generative Adversarial Networks (GANs)
GANs consist of two neural networks—a generator and a discriminator—that compete against each other in a process known as adversarial training.
Key Features:
- The generator creates synthetic data that mimics real data.
- The discriminator evaluates whether the generated data is real or fake.
- The networks improve over time, producing highly realistic outputs.
Applications:
- Image generation (e.g., AI-generated artwork)
- Deepfake technology (e.g., realistic face-swapping)
- Data augmentation (e.g., generating synthetic medical images for training models)
6. Applications of Neural Networks
Neural networks have revolutionized various industries by enabling machines to process and interpret complex data efficiently. Their ability to learn patterns and make predictions has led to significant advancements in different domains. Below is a detailed explanation of how neural networks are applied in various fields.
6.1 Healthcare
Neural networks play a crucial role in improving medical diagnosis, treatment planning, and drug discovery. With the ability to analyze large volumes of medical data, they enhance the accuracy and efficiency of healthcare systems.
Key Applications:
- Disease Prediction & Diagnosis
- Deep learning models analyze patient records, medical images, and genetic data to detect diseases early.
- Example: AI models can predict diseases like cancer, diabetes, and Alzheimer’s by analyzing medical images and patient histories.
- CNNs are widely used in MRI and X-ray analysis to detect tumors, fractures, or infections.
- Medical Image Analysis
- Neural networks process radiology images (X-rays, CT scans, MRIs) to identify abnormalities.
- Example: Google’s DeepMind developed an AI model that detects eye diseases from retinal scans.
- Drug Discovery & Development
- AI accelerates the drug discovery process by predicting molecular interactions.
- Example: Deep learning models help identify potential drug candidates for diseases like COVID-19.
- Personalized Treatment Plans
- AI-driven models analyze patient history and genetic information to suggest tailored treatments.
- Example: IBM Watson for Oncology recommends personalized cancer treatment plans based on medical literature.
6.2 Finance
Financial institutions use neural networks to improve security, predict market trends, and manage risks.
Key Applications:
- Fraud Detection
- Neural networks analyze transaction patterns to identify fraudulent activities.
- Example: Banks like JPMorgan and PayPal use AI to detect credit card fraud by flagging unusual transactions.
- Stock Market Prediction
- AI models analyze historical stock data, news trends, and market sentiment to predict price movements.
- Example: Hedge funds use deep learning for high-frequency trading and risk assessment.
- Credit Scoring & Risk Assessment
- Neural networks assess a person’s creditworthiness based on financial history.
- Example: FICO scores use AI to determine loan eligibility and interest rates.
- Automated Trading Systems
- AI-powered trading bots execute trades based on market trends.
- Example: Goldman Sachs and other firms use neural networks for automated trading.
6.3 Autonomous Vehicles
Neural networks are critical in enabling self-driving cars by helping them perceive and interpret the environment.
Key Applications:
- Object Detection & Recognition
- CNNs process real-time camera feeds to detect pedestrians, vehicles, and road signs.
- Example: Tesla’s Autopilot uses deep learning to detect and respond to traffic signals.
- Path Planning & Navigation
- Recurrent Neural Networks (RNNs) and LSTMs predict optimal driving paths by analyzing real-time traffic data.
- Example: Waymo’s self-driving cars use deep learning to predict vehicle movements.
- Collision Avoidance
- AI models analyze sensor data to prevent accidents.
- Example: Automatic Emergency Braking (AEB) in modern cars detects obstacles and applies brakes.
6.4 Natural Language Processing (NLP)
Neural networks power applications that process and generate human language, improving communication between humans and machines.
Key Applications:
- Chatbots & Virtual Assistants
- NLP-based chatbots handle customer queries in real-time.
- Example: ChatGPT, Siri, Google Assistant use deep learning for conversational AI.
- Machine Translation
- RNNs and Transformers translate text between languages.
- Example: Google Translate uses AI to improve translation accuracy.
- Sentiment Analysis
- AI models analyze social media posts, reviews, and feedback to determine public sentiment.
- Example: Businesses use AI to gauge customer opinions about products.
- Speech Recognition
- AI models convert spoken words into text.
- Example: Amazon Alexa and Microsoft Cortana use NLP for speech recognition.
6.5 Computer Vision
Computer vision applications use neural networks to interpret and analyze visual data.
Key Applications:
- Face Recognition
- AI detects and verifies faces in images and videos.
- Example: Apple’s Face ID unlocks iPhones using deep learning.
- Image Classification
- CNNs classify images into different categories.
- Example: AI can differentiate between cats and dogs in images.
- Video Analysis & Surveillance
- AI analyzes real-time video feeds to detect suspicious activities.
- Example: AI-powered security cameras can identify intruders in restricted areas.
- Augmented Reality (AR) & Virtual Reality (VR)
- AI enhances user experiences in gaming and simulations.
- Example: Snapchat filters use CNNs for real-time face tracking.
6.6 Other Applications
Neural networks are also applied in various other industries:
1. Agriculture
- AI-powered drones monitor crop health and detect diseases.
- Smart irrigation systems use AI to optimize water usage.
2. Manufacturing
- AI-powered robots automate assembly lines.
- Predictive maintenance prevents machinery failures.
3. Cybersecurity
- AI detects malware and cybersecurity threats.
- Neural networks analyze network traffic for anomalies.
4. Entertainment & Media
- AI recommends movies and music on platforms like Netflix and Spotify.
- AI-generated content, such as deepfake videos, is used in creative media.
Key Takeaways
Neural networks play a vital role in deep learning and artificial intelligence. By mimicking the structure of the human brain, they enable computers to recognize patterns, make decisions, and solve complex problems. Understanding the structure, activation functions, training process, and different types of neural networks provides a strong foundation for further exploration into deep learning.
This module serves as an introduction to neural networks, preparing students for more advanced topics such as deep learning architectures, optimization techniques, and real-world applications.
Next Blog- Python Implementation of Neural Network for Classification
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
