Activation Functions in Deep Learning –
1. Introduction to Activation Functions
In deep learning, an activation function is a mathematical function applied to the output of a neuron to determine whether it should be activated or not. It introduces non-linearity into the network, allowing it to learn complex patterns from data. Without activation functions, a neural network would behave like a simple linear regression model, incapable of solving problems such as image recognition, speech processing, and natural language understanding.
Why Are Activation Functions Important?
Activation functions play a crucial role in the working of neural networks. They determine how a neuron processes input signals and whether it should pass a signal to the next layer. Without activation functions, neural networks would simply perform linear transformations, limiting their ability to learn complex patterns. Let's break down their importance in detail:
1. Introducing Non-Linearity
Non-linearity refers to a relationship between input and output where the change in output is not directly proportional to the change in input. In simpler terms, a function is non-linear if it cannot be represented by a straight line.
Why is non-linearity important?
Most real-world problems involve complex patterns that cannot be captured using simple linear functions. Activation functions introduce non-linearity, allowing neural networks to learn intricate relationships between inputs and outputs.
Example
A linear model (without activation functions) can only learn functions of the form:
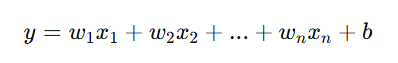
This means it cannot model complex decision boundaries like those needed for image recognition, speech processing, or language translation.
However, with activation functions like ReLU or sigmoid, neural networks can approximate highly non-linear relationships between input and output.
2. Enabling Deep Networks
Deep learning relies on multiple layers of neurons to learn hierarchical representations of data. However, if there were no activation functions, stacking multiple layers would not increase the expressive power of the model.
Why?
Without activation functions, each layer would just apply a linear transformation to the previous layer, leading to an equivalent single-layer perceptron. This means a deep network without activation functions behaves just like a single-layer network, making deep learning ineffective.
Example
Imagine trying to classify images of dogs and cats. A shallow network may only capture basic pixel patterns, but a deep network learns:
- Early layers → Edges and textures
- Mid layers → Shapes and structures
- Deep layers → Complex features like eyes, nose, or fur patterns
3. Controlling Gradient Flow
Neural networks train using backpropagation, where gradients are computed and used to update weights. Activation functions influence how gradients flow through the network, affecting learning speed and stability.
Issues Without Proper Activation Functions
- Vanishing Gradient Problem
- If the activation function squashes values too much (like sigmoid or tanh in deep networks), gradients become extremely small.
- This means lower layers receive almost no updates, slowing or stopping learning.
- Solution: ReLU activation helps prevent vanishing gradients by not saturating for positive values.
- Exploding Gradient Problem
- When gradients grow too large (common in deep networks), weight updates become unstable, leading to divergent learning.
- Solution: Normalization techniques like batch normalization and activation functions like Leaky ReLU help mitigate this.
4. Ensuring Efficient Computation
Some activation functions improve training efficiency by ensuring stable gradient updates and preventing unnecessary computations.
How?
ReLU (Rectified Linear Unit) is computationally efficient because it involves a simple operation:
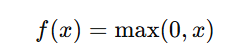
This avoids expensive exponentials (as in sigmoid/tanh), making it faster for large-scale neural networks.
- Softmax Activation normalizes multi-class outputs into probabilities, making it efficient for classification problems.
Example
A deep neural network with millions of neurons benefits from faster activations like ReLU, allowing it to scale efficiently for real-time applications (e.g., self-driving cars, facial recognition).
2. Types of Activation Functions
Activation functions are broadly classified into two categories:
- Linear Activation Functions
- Non-Linear Activation Functions
Let’s explore these in detail.
3. Linear Activation Function
Introduction to the Linear Activation Function
A linear activation function is the most basic type of activation function used in neural networks. In this function, the output is a scaled version of the input, meaning the relationship between input and output is purely linear.
While simple, it has significant limitations, which is why non-linear activation functions are preferred for deep learning.
Mathematical Formula
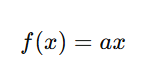
where:
- x is the input to the neuron,
- a is a constant multiplier (also known as the gain factor),
- f(x) is the output.
Example
If a=1, the function simplifies to:
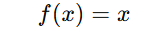
This means the output is exactly the same as the input, creating a direct proportionality.
Characteristics
- Range: (−∞,+∞)
- The output can take any real value, which makes it suitable for regression problems but not classification.
- Linearity:
- The function maintains a directly proportional relationship between input and output.
- Derivatives:
The derivative of f(x)=ax is a constant:
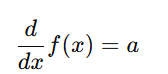
- This means the gradient is always constant and does not depend on the input.
Why the Linear Activation Function Is Not Used in Deep Networks
Lack of Non-Linearity
The biggest issue with the linear activation function is that it does not introduce non-linearity.
If we stack multiple layers using a linear activation function, the entire network collapses into a single-layer model, because:
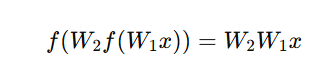
which is still linear.
No matter how many layers we add, the final output is just a linear transformation of the input.
Limited Learning Capacity
- Since the function is linear, it cannot model complex decision boundaries required for tasks like image recognition or language processing.
- Non-linear activation functions (like ReLU or Sigmoid) help neural networks learn abstract features, which is why they are preferred.
Gradient Descent Becomes Ineffective
- The derivative of a linear activation function is constant (aaa), which means the gradient remains the same during backpropagation.
- In deep networks, this prevents the network from adjusting weights dynamically, slowing down learning.
When Is the Linear Activation Function Used?
Although the linear activation function is rarely used in hidden layers, it has some specific use cases:
1. Regression Problems
- In linear regression models, the output is a continuous value, making a linear activation function suitable for the output layer.
- Example: Predicting house prices based on features like size and location.
2. Simpler Models with No Need for Non-Linearity
- Some machine learning models do not require deep feature extraction, so a linear activation function may be acceptable.
- Example: A basic neural network for financial predictions where a linear relationship is sufficient.
3. Specialized Cases in Reinforcement Learning
- In some reinforcement learning models, a linear activation function is used when outputs need to be continuous and unbounded.
4. Non-Linear Activation Functions
1. Introduction to Non-Linear Activation Functions
In deep learning, neural networks need to model complex relationships between inputs and outputs. If all activation functions were linear, no matter how many layers were added, the network would still behave as a single-layer perceptron.
To introduce learning capability and generalization, we use non-linear activation functions. These functions allow neural networks to learn patterns, capture dependencies, and represent hierarchical structures.
A non-linear activation function introduces a non-linear transformation to the input, enabling the network to solve complex tasks such as image recognition, natural language processing, and speech recognition.
2. Why Are Non-Linear Activation Functions Important?
- Enables Complex Learning: Allows the network to learn non-trivial patterns and solve problems that cannot be solved by a single-layer perceptron.
- Introduces Non-Linearity: Helps model real-world relationships, which are often non-linear.
- Improves Model Expressiveness: A network with non-linear activations can approximate any function (Universal Approximation Theorem).
- Prevents the Network from Collapsing into a Linear Model: Stacking multiple layers with non-linear activations provides meaningful depth.
3. Common Non-Linear Activation Functions
Sigmoid Activation Function
The sigmoid activation function is one of the most commonly used activation functions in machine learning and deep learning, particularly for binary classification problems. It is a smooth, S-shaped (sigmoid) curve that transforms input values into a probability-like output ranging between 0 and 1.
Since the sigmoid function squashes all inputs to a limited range, it is particularly useful in scenarios where the outputs need to represent probabilities, such as logistic regression and binary classification tasks.
Mathematical Formula
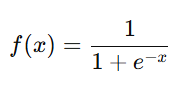
where:
- x is the input value,
- e is Euler’s number (~2.718),
- The function transforms x into a value between 0 and 1.
Characteristics-
Range(0,1)(0,1)(0,1)
The output is always between 0 and 1, which is useful for probability estimation.
S-shaped (Sigmoid Curve)
The function smoothly transitions between values, creating a soft threshold around x=0x = 0x=0.
Probabilistic Interpretation
The output can be interpreted as a probability, making it useful for classification tasks.
Derivative of the Sigmoid Function
The derivative is given by:
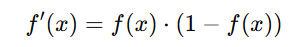
This is useful in gradient-based optimization techniques, as it helps compute weight updates.
Advantages of the Sigmoid Function
- Useful in Classification Problems
- Since the output is between 0 and 1, it is commonly used in binary classification models (e.g., spam detection, fraud detection).
- Smooth and Differentiable
- The function is continuous and differentiable, which allows smooth weight updates in gradient descent optimization.
- Probability Interpretation
- The sigmoid function outputs values that can be interpreted as probabilities, making it suitable for logistic regression and deep learning classification problems.
Disadvantages of the Sigmoid Function
- Vanishing Gradient Problem
- For very large (x≫1x \gg 1x≫1) or very small (x≪−1x \ll -1x≪−1) values of x, the derivative of the sigmoid function approaches zero.
- This causes gradients to become extremely small, leading to slow learning or stagnation in deep networks.
- Computationally Expensive
- The function requires an exponentiation operation, which is computationally costly compared to other activation functions like ReLU.
- Not Zero-Centered
- Since the output of sigmoid is always positive, gradient updates may not be balanced, leading to slow convergence.
Use Cases of the Sigmoid Function
1. Output Layer of Binary Classification Models
- Logistic regression and binary classifiers use the sigmoid function in the final layer to map the predictions to a probability between 0 and 1.
2. Probability Estimation
- In reinforcement learning and probabilistic models, sigmoid is used to estimate probabilities for decision-making.
3. Neural Networks (Limited Usage)
- It is sometimes used in hidden layers of small networks, but ReLU and its variants are preferred for deeper networks due to the vanishing gradient issue.
Tanh (Hyperbolic Tangent) Activation Function
The tanh (hyperbolic tangent) activation function is a commonly used non-linear activation function in deep learning. It is similar to the sigmoid function, but with an important difference: tanh is zero-centered, meaning its output values range from -1 to 1 instead of 0 to 1.
This property makes tanh more effective in hidden layers than sigmoid, as it allows balanced gradient updates, preventing issues related to shifting activations.
Mathematical Formula
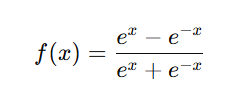
where:
- e is Euler’s number (~2.718),
- x is the input to the function.
The derivative of tanh is given by:
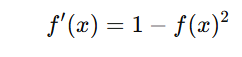
Characteristics-
Range
(−1,1)(-1, 1)(−1,1)
Unlike the sigmoid function, which outputs values between 0 and 1, tanh maps inputs to a range of -1 to 1, which allows negative values.
Zero-Centered
The output is centered around zero, meaning that the mean activation value is close to zero. This helps in faster convergence during training because gradients remain balanced, reducing bias in weight updates.
Steep S-Shaped Curve
Similar to sigmoid, tanh has an S-shaped curve, but it is steeper, allowing stronger gradients in most regions.
Advantages of Tanh Activation Function-
- Better than Sigmoid for Hidden Layers
- Since tanh produces both positive and negative values, it helps maintain a zero-centered mean, which improves training efficiency.
- Stronger Gradients than Sigmoid
- The derivative of tanh is larger than that of sigmoid in most regions, leading to faster weight updates and better learning performance.
- Smooth and Differentiable
The function is continuous and differentiable, making it useful for backpropagation-based optimization.
Disadvantages of Tanh Activation Function-
- Vanishing Gradient Problem
- For very large or very small input values, the function saturates, meaning the derivative becomes close to zero.
- This leads to slow learning, especially in deep networks.
- Computational Cost
Like sigmoid, tanh requires exponentiation operations, which are computationally more expensive than ReLU.
Use Cases of Tanh Activation Function-
1. Hidden Layers of Neural Networks
Tanh is commonly used in hidden layers of deep networks because it provides zero-centered outputs, improving training efficiency.
2. Recurrent Neural Networks (RNNs)
Since tanh allows both negative and positive activations, it is frequently used in RNNs and LSTMs for handling sequential data.
3. Image Processing
- Tanh can be used in certain image processing tasks, where negative values provide better feature extraction.
ReLU (Rectified Linear Unit) Activation Function
The ReLU (Rectified Linear Unit) activation function is the most commonly used activation function in deep learning, especially in hidden layers of neural networks. It is preferred because of its simplicity, efficiency, and ability to mitigate the vanishing gradient problem, which affects earlier activation functions like sigmoid and tanh.
Mathematical Formula
The ReLU function is defined as:
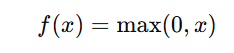
This means:
- If x>0, then f(x)=x (linear response).
- If x≤0, then f(x)=0(inactive neuron).
The derivative of ReLU is:
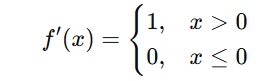
Unlike sigmoid and tanh, the derivative of ReLU does not vanish for large positive values, which helps speed up learning.
Characteristics of ReLU-
Range
[0,∞)
ReLU only outputs non-negative values, meaning it does not produce negative activations.
Sparsity
ReLU outputs zero for all negative inputs, meaning some neurons become inactive. This helps make computations more efficient by reducing unnecessary calculations.
Piecewise Linear
- For positive values, ReLU behaves like a linear function.
- For negative values, it acts as a constant zero function.
Advantages of ReLU-
- Solves the Vanishing Gradient Problem
- Unlike sigmoid and tanh, which squash values into small ranges, ReLU allows large gradients for positive inputs.
- This prevents gradients from becoming too small, ensuring faster learning.
- Computational Efficiency
- The function is extremely simple to compute—just applying a threshold at zero.
- No expensive exponential operations like in sigmoid or tanh.
- Sparse Activation
- By outputting zero for negative inputs, ReLU makes networks more efficient because only a subset of neurons is active at any given time.
- Works Well in Deep Networks
- ReLU is particularly useful for deep neural networks, where sigmoid and tanh struggle due to gradient issues.
Disadvantages of ReLU-
- Dying ReLU Problem
- If many neurons receive negative inputs, they always output zero, becoming permanently inactive.
- This means that certain neurons never contribute to learning.
- Leaky ReLU and Parametric ReLU were developed to address this issue.
- Unbounded Output for Positive Values
- Since ReLU has no upper limit, it can produce very large activations, leading to potential instability in some cases.
Use Cases of ReLU-
1. Hidden Layers of Deep Neural Networks
- ReLU is the default choice for activation functions in deep learning models because of its efficiency and ability to handle vanishing gradients.
2. Computer Vision Tasks
- Used in CNNs (Convolutional Neural Networks) for tasks like image recognition and object detection.
3. Natural Language Processing (NLP)
- Applied in transformer models, RNNs, and LSTMs to improve learning efficiency.
4. Reinforcement Learning
- Helps deep reinforcement learning models learn complex behaviors efficiently.
Leaky ReLU Activation Function
Introduction
The Leaky ReLU (Leaky Rectified Linear Unit) activation function is a modified version of ReLU that addresses its major drawback—the dying ReLU problem. Unlike standard ReLU, which outputs zero for all negative values, Leaky ReLU allows small negative values instead of setting them to zero. This prevents neurons from becoming completely inactive during training.
Mathematical Formula
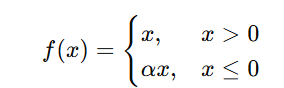
Where α (alpha) is a small positive constant (typically 0.01 or 0.1).
- If x>0, the function behaves like a linear function (f(x)=x.
- If x≤0, instead of zero, it outputs a small fraction of x (e.g., 0.01x).
The derivative of Leaky ReLU is:
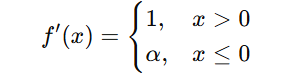
Since α is nonzero, it ensures that gradients never become exactly zero, preventing neurons from dying.
Characteristics of Leaky ReLU-
Range
(−∞,∞)
Leaky ReLU allows negative outputs, unlike standard ReLU, which is restricted to [0, ∞).
Small Negative Slope
For negative inputs, Leaky ReLU outputs small nonzero values instead of zero, helping neurons stay active.
Piecewise Linear
- For positive values, it behaves like ReLU.
- For negative values, it has a small negative slope instead of being zero.
Advantages of Leaky ReLU-
- Prevents the Dying ReLU Problem
- In ReLU, neurons can become permanently inactive when they output zero for negative inputs.
- Leaky ReLU ensures a small gradient for negative values, keeping neurons active.
- Maintains Efficiency
- Like ReLU, it has a simple and efficient computation.
- No complex exponentiation like sigmoid or tanh.
- Faster Convergence
- Helps deep networks learn faster by avoiding inactive neurons.
- Works well in very deep architectures.
Disadvantages of Leaky ReLU-
- Still Unbounded for Positive Inputs
- Since positive outputs can grow infinitely, it can cause unstable activations.
- Hyperparameter Sensitivity
- The choice of α\alpha (negative slope) affects performance.
- Too small a value can make it behave like ReLU, while too large a value may distort learning.
- Not Universally Better than ReLU
- In some cases, simple ReLU still performs better, especially in architectures where dying ReLU is not an issue.
Use Cases of Leaky ReLU-
1. Deep Networks with ReLU Issues
- Used in deep neural networks where ReLU leads to dead neurons.
2. Image Recognition
- Common in CNNs (Convolutional Neural Networks) to improve feature learning.
3. GANs (Generative Adversarial Networks)
- Helps in stabilizing adversarial training.
4. NLP and Time-Series Models
- Used in RNNs, LSTMs, and transformers where avoiding zero activations is beneficial.
Softmax Activation Function
Introduction
The Softmax activation function is widely used in multi-class classification problems. It converts raw scores (logits) from the output layer into probabilities, making it useful when an input belongs to one of several possible classes. Each output value represents the probability of the input belonging to a particular class.
Mathematical Formula-
For a given input vector z=[z1,z2,...,zn] representing raw scores (logits), the Softmax function is calculated as:
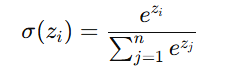

This formula normalizes the raw outputs into probabilities.
Characteristics of Softmax-
Probability Distribution
- The sum of all outputs is always 1, making them interpretable as probabilities.
- Each output value represents the likelihood of an input belonging to a specific class.
Exponentially Scales Inputs
- Large input values lead to higher probabilities, while small values approach zero.
Differentiable and Smooth
- The function is smooth and continuous, making it useful for gradient-based optimization.
Advantages of Softmax-
1. Converts Scores into Probabilities
- Makes raw output values meaningful by turning them into probabilities.
- Helps in decision-making in classification tasks.
2. Useful for Multi-Class Classification
- Ensures that each sample belongs to one of multiple categories with a probability distribution.
- The highest probability class is usually chosen as the final prediction.
3. Works Well with Cross-Entropy Loss
- Softmax is often paired with categorical cross-entropy loss, which is efficient for multi-class classification.
Disadvantages of Softmax-
1. Sensitive to Large Input Values
- If the input logits are large, the exponential function can produce very large numbers, causing exploding gradients.
- This issue can be reduced using normalization techniques, such as batch normalization.
2. Can Cause Vanishing Gradients
- If one value dominates the others, the gradients for smaller values become almost zero, making learning difficult.
3. Not Ideal for Binary Classification
- For binary classification, sigmoid activation is a better choice because Softmax is unnecessary when only two categories exist.
Use Cases of Softmax-
1. Multi-Class Classification Problems
- Used in the output layer of models where an input belongs to one of several categories (e.g., classifying images into 10 categories).
2. Natural Language Processing (NLP)
- In text classification, Softmax helps assign probabilities to different categories (e.g., spam vs. non-spam emails).
3. Image Recognition
- Convolutional Neural Networks (CNNs) use Softmax in the final layer to classify images into multiple categories.
4. Reinforcement Learning
- Used in policy networks to determine the probability of taking different actions.
Swish Activation Function
Introduction
The Swish activation function is a smooth, self-gated function introduced by researchers at Google. It is an improvement over ReLU, offering better performance in deep networks by avoiding issues like dying neurons.
Swish is non-monotonic, meaning it does not increase or decrease consistently, allowing neural networks to adapt better to complex patterns in data.
Mathematical Formula
The Swish function is defined as:
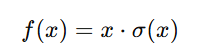
where:
σ(x) is the sigmoid function,
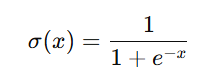
- The function behaves like ReLU for large values of x but allows small negative values instead of forcing them to zero.
Characteristics of Swish-
1. Smooth and Differentiable
- Unlike ReLU, which has a sharp transition at zero, Swish is smooth and continuously differentiable.
- This smoothness allows better gradient flow, improving deep network training.
2. Self-Gated Behavior
- The function automatically decides how much each input should be scaled, making it more adaptive.
3. Non-Monotonic
- Unlike ReLU, Swish does not strictly increase or decrease, which helps in capturing complex patterns.
Advantages of Swish-
1. Avoids Dying Neurons
- In ReLU, negative inputs are mapped to zero, leading to "dead neurons."
- Swish allows small negative values, preventing this issue.
2. Outperforms ReLU in Deep Networks
- Swish has been found to work better than ReLU in deep architectures, as it enables better gradient flow.
- This helps networks learn more effectively in complex tasks.
3. Smooth Activation Function
- The smooth nature of Swish allows gradients to propagate efficiently, reducing training issues.
Disadvantages of Swish-
1. Computationally Expensive
- Unlike ReLU, which only requires a thresholding operation, Swish involves multiplication and exponentiation (due to the sigmoid function).
- This makes it slower to compute, especially in resource-constrained environments.
2. Not Always Superior to ReLU
- While Swish performs better in deep networks, it may not provide significant benefits for shallow architectures.
- In some cases, ReLU is still preferred due to its simplicity.
Use Cases of Swish-
1. Deep Neural Networks
- Swish is beneficial for very deep architectures where gradient flow is critical.
- Used in models like EfficientNet for image recognition tasks.
2. Natural Language Processing (NLP)
- Works well in transformer-based models like BERT and GPT, where smooth activations improve long-range dependencies.
3. Reinforcement Learning
- Swish has been used in policy gradient methods, improving stability in agent training.
How to Choose the Right Activation Function?
| Activation Function | Use Case |
|---|---|
| Sigmoid | Binary classification output layers |
| Tanh | Hidden layers in shallow networks |
| ReLU | Deep neural networks |
| Leaky ReLU | Preventing dead neurons in deep networks |
| Softmax | Multi-class classification output layers |
| Swish | Very deep networks |
Key Takeaways of Activation Functions in Deep Learning
- Purpose: Activation functions introduce non-linearity, enabling neural networks to learn complex patterns and relationships.
- Types of Activation Functions:
- Linear: No non-linearity; unsuitable for deep networks.
- Non-Linear: Essential for deep learning models.
- Common Activation Functions:
- Sigmoid: Outputs between (0,1); used for probability-based tasks but suffers from vanishing gradients.
- Tanh: Outputs between (-1,1); better than sigmoid but still prone to vanishing gradients.
- ReLU (Rectified Linear Unit): Most widely used; avoids vanishing gradients but can suffer from dead neurons (dying ReLU problem).
- Leaky ReLU: Improves ReLU by allowing small negative values, preventing dead neurons.
- Softmax: Used in classification tasks to output probabilities for multiple classes.
- Swish & GELU: Advanced activation functions that improve learning efficiency.
- Choosing the Right Activation Function:
- For hidden layers: ReLU and its variants are preferred.
- For output layers:
- Sigmoid (binary classification)
- Softmax (multi-class classification)
- Linear (regression tasks)
- Impact on Training: Activation functions influence gradient flow, learning speed, and convergence stability.
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
