Introduction

Perceptrons and Multi-Layer Perceptrons (MLPs) are fundamental building blocks of artificial neural networks. They are used for pattern recognition, classification, and function approximation in machine learning.

• Perceptron is the simplest type of artificial neural network, introduced by Frank Rosenblatt in 1958. It is a single-layer neural network that can solve linearly separable problems.
• Multi-Layer Perceptron (MLP) is an extension of the perceptron that consists of multiple layers of neurons, allowing it to solve non-linearly separable problems.

Perceptron

2.1 Structure of a Perceptron

A Perceptron consists of several components that work together to process inputs and generate an output. It mimics the functioning of a biological neuron, where the dendrites receive inputs, the soma processes the information, and the axon sends an output signal.

Components of a Perceptron:

1. Inputs (x₁, x₂, ..., xₙ)
   • These are the features or raw data values fed into the perceptron.
   • Example: If a perceptron is used for spam detection, the inputs could be features like the number of spam keywords, the sender's email reputation, etc.
2. Weights (w₁, w₂, ..., wₙ)
   • Each input is assigned a weight that represents its significance in determining the output.
   • The weights are learned and adjusted during training.
3. Bias (b)
   • A constant value that helps shift the decision boundary and improve the learning capability of the model.
   • The bias prevents the model from always passing through the origin.
4. Summation Function (Σ)
   • The perceptron computes the weighted sum of inputs as:

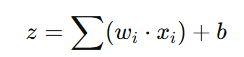
• This step combines all inputs and their respective weights.

        5. Activation Function

• Applies a mathematical function to determine the final output.

• A step function (threshold function) is typically used in a perceptron:

  

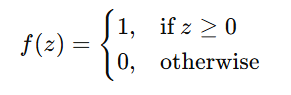
  If the weighted sum is greater than or equal to 0, the perceptron outputs 1; otherwise, it outputs 0.

• Diagram Representation of a Perceptron

   rust
         
         x₁ ---->  | W₁  |         x₂ ---->  | W₂  | ---> Summation ---> Activation ---> Output (0 or 1)         x₃ ---->  | W₃  |         ...               xₙ ---->  | Wₙ  |               + Bias (b)

2.2 Working of a Perceptron

A perceptron operates in four simple steps:

Step 1: Receive Inputs

• The perceptron takes multiple inputs (x₁, x₂, ..., xₙ).

Step 2: Compute Weighted Sum

• It multiplies each input by its corresponding weight and adds them together, along with the bias term:

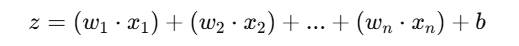
Step 3: Apply Activation Function

• The step activation function is applied to determine the final output:

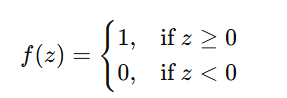
Step 4: Generate Output

• The perceptron produces a binary output (0 or 1), which is used for classification.

  

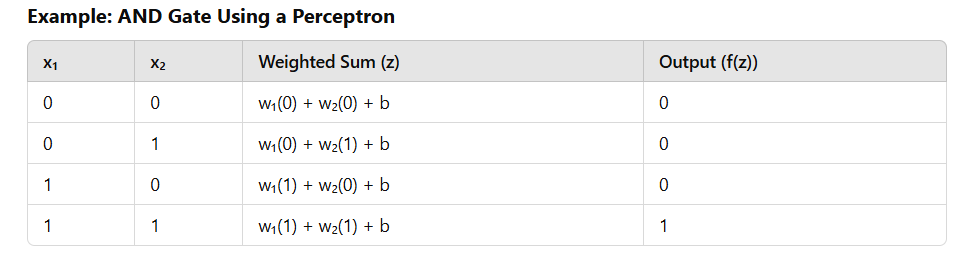
2.3 Perceptron Learning Algorithm

The perceptron learns by adjusting its weights based on the training data. The learning process ensures that the perceptron correctly classifies inputs over time.

Steps in the Perceptron Learning Algorithm:

1. Initialize Weights and Bias

• Set the weights and bias to small random values.

2. For Each Training Sample:

• Compute the predicted output (ŷ) using:

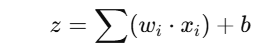
Apply the step activation function to obtain the final output.

3. Compare Prediction with Actual Output (y)

• Check if the predicted output (ŷ) matches the actual output (y).

4. Update Weights if Prediction is Incorrect
 

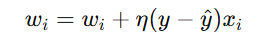
where:

1. η is the learning rate.
2. y is the actual output.
3. y is the predicted output.
4. Repeat until all samples are classified correctly or a stopping condition is met.

Example of Weight Update

• Suppose:
  • Learning rate (η) = 0.1
  • Initial weights: w₁ = 0.5, w₂ = -0.3
  • Bias b = 0.2
  • Input: (x₁ = 1, x₂ = 1)
  • Actual output y = 1
  • Predicted output ŷ = 0 (incorrect classification)

Weight Update Formula:

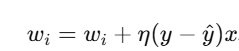
• New Weights:
  • w1=0.5+0.1(1−0)(1)=0.6
  • w2=−0.3+0.1(1−0)(1)=−0.2
• New Bias:
  • b=b+η(y−y^)
  • b=0.2+0.1(1−0)=0.3

2.4 Limitations of Perceptron

Despite its simplicity, the perceptron has several limitations:

1. Can Only Solve Linearly Separable Problems

• The perceptron works well with problems that can be separated by a straight line, such as AND and OR functions.

• It fails to solve problems like XOR, which require a non-linear decision boundary.

  Example: XOR Problem

  • XOR cannot be separated by a straight line:

    x₁	x₂	XOR Output
    0	0	0
    0	1	1
    1	0	1
    1	1	0

  • Since there is no single line that can separate the 1s and 0s, a single perceptron fails to classify XOR correctly.

2. Uses a Step Function

• The step activation function is not differentiable, making it impossible to use gradient-based learning (e.g., backpropagation in deep networks).
• Modern neural networks use sigmoid, ReLU, or softmax activation functions instead.

3. Cannot Handle Complex Patterns

• The perceptron cannot learn patterns requiring multiple layers.
• To solve XOR and complex problems, we need multi-layer perceptrons (MLPs) with hidden layers.

Key Takeaways

• Perceptrons solve only linearly separable problems.
• Key components: inputs, weights, bias, summation, activation.
• Uses a step function for binary classification.
• Learning updates weights based on errors.
• Cannot solve XOR or complex patterns.
• Multi-layer perceptrons (MLPs) overcome perceptron limitations.

Next Blog- Multi-Layer Perceptron (MLP)