Reinforcement Learning February 02 ,2025

Value-Based Methods

Value-based reinforcement learning focuses on estimating value functions to determine the best policy. These methods help agents make optimal decisions by learning which states or actions yield the highest rewards.

1. Introduction to Value-Based Methods

Reinforcement Learning (RL) involves an agent interacting with an environment to maximize cumulative rewards. In value-based methods, the agent does not learn a direct policy (which action to take). Instead, it learns a value function, which estimates the long-term expected reward for different states or actions.

Once the agent has a good estimate of these values, it selects the optimal action by choosing the one with the highest value.

2. Key Concepts in Value-Based Methods

a. State Value Function (V(s))

The state value function represents the expected cumulative reward an agent will receive if it starts at a given state ss and follows a policy π. It is mathematically defined as:

Eπ → Expectation (average) over all possible rewards while following policy π.
γ → Discount factor (0 ≤ γ ≤ 1) that determines the importance of future rewards.
Rt → Reward received at time step tt.

Interpretation:

If V(s) is high, it means the agent expects high rewards from that state.
The agent should prefer states with higher V(s) values.

b. Action-Value Function (Q(s,a))

The action-value function measures the expected return when an agent takes a specific action aa in state ss, and then follows policy π\pi. It is given by:

Q(s,a) tells the agent how good it is to take action a in state s.
The optimal action is the one that maximizes Q(s,a).

Relationship between V(s) and Q(s,a):

This means the best state value is determined by the best action from that state.

c. Bellman Equation

The Bellman Equation is a recursive formula that helps update value functions. It states that the value of a state is equal to the immediate reward plus the discounted future value.

For the state-value function:

For the action-value function:

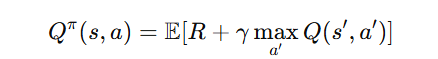
This equation allows RL agents to iteratively update their value estimates.

3. Types of Value-Based Methods

Value-based RL can be categorized into different approaches:

a. Dynamic Programming (DP) Methods

Requires a complete model of the environment’s transition probabilities.
Uses the Bellman Equation for iterative updates.
Examples:
- Value Iteration: Repeatedly updates V(s) values to find the optimal value function.
- Policy Iteration: Alternates between evaluating and improving the policy.

Limitation: DP methods are computationally expensive and require full knowledge of the environment.

b. Monte Carlo Methods

Learn from complete episodes by averaging observed returns.
No need for a transition model, making it more model-free than DP.
Key Idea: Instead of updating values after every step, Monte Carlo methods wait until the end of an episode and then update based on the total rewards received.

Limitation: Slow convergence, as updates occur only at the end of an episode.

c. Temporal Difference (TD) Learning

TD methods combine ideas from Monte Carlo and Dynamic Programming:

Unlike Monte Carlo, TD updates after every step (not at the end of an episode).
Unlike DP, TD does not require a transition model.

Key TD Algorithms:

TD(0) Algorithm: Updates value functions incrementally.
SARSA: On-policy learning method.
Q-Learning: Off-policy learning method.

4. Popular Value-Based Algorithms

a. SARSA (On-Policy Learning)

SARSA stands for State-Action-Reward-State-Action. It updates the Q-values using:

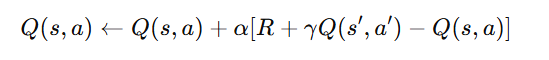
Learns based on the actions it actually takes (on-policy).
Good for safe learning but may not always find the best policy.

b. Q-Learning (Off-Policy Learning)

Q-learning is an off-policy algorithm, meaning it updates Q-values using the maximum possible future Q-value, rather than following its current policy:

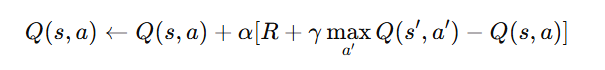
More flexible than SARSA.
Converges to the optimal policy in many cases.

c. Deep Q-Networks (DQN)

DQN is an extension of Q-learning using deep neural networks to handle high-dimensional environments. It introduced two key improvements:

Experience Replay:
- Stores past experiences and randomly samples them to break correlation in training.
Target Networks:
- Uses a separate, slowly updated network to stabilize Q-value estimates.

DQN has been successfully applied to games like Atari.

5. Advantages of Value-Based Methods

Works well for discrete action spaces.
Efficient for problems with well-defined state transitions.
Converges to optimal policies in deterministic environments.

6. Limitations of Value-Based Methods

Struggles with continuous action spaces (needs discretization).
Cannot easily learn stochastic policies (uncertainty in decisions).
Requires extensive exploration to find the best policy.

Got it! Here are the key takeaways without emojis:

Key Takeaways: Value-Based Methods in Reinforcement Learning

Value-Based Learning focuses on estimating value functions rather than directly learning policies.
State Value Function (V(s)V(s)) estimates the expected reward from a given state, while Action-Value Function (Q(s,a)Q(s, a)) evaluates the expected return of taking a specific action in a state.
Bellman Equation provides a recursive way to update value estimates, forming the foundation of many reinforcement learning algorithms.

Types of Value-Based Methods:

Dynamic Programming (DP) – Requires complete knowledge of the environment but is computationally expensive.
Monte Carlo Methods – Learn from complete episodes, leading to slow updates but good convergence.
Temporal Difference (TD) Learning – Updates values after each step, combining the benefits of DP and Monte Carlo methods.

Popular Algorithms:

SARSA (On-Policy) – Learns from the actions taken by the agent.
Q-Learning (Off-Policy) – Learns the best possible actions even if they are not executed by the agent.
Deep Q-Networks (DQN) – Uses deep learning to handle high-dimensional state spaces.

Advantages: