Introduction to Policy Gradient Methods
Policy Gradient Methods are a class of reinforcement learning (RL) techniques that directly learn an optimal policy without relying on value functions. These methods are widely used in advanced RL applications like robotics, game AI, autonomous driving, and financial trading.
What Are Policy Gradient Methods?
In reinforcement learning, an agent interacts with an environment and learns to take actions to maximize a long-term reward. There are two primary ways to learn an optimal behavior:
- Value-Based Methods: These methods, like Q-learning and Deep Q Networks (DQN), learn a value function that estimates how good an action is in a given state. The policy is then indirectly derived from this value function.
- Policy-Based Methods (Policy Gradients): Instead of learning value functions, these methods directly learn a policy that maps states to actions. They adjust the policy parameters to maximize rewards, often using gradient ascent.
Key Idea of Policy Gradients
- The agent follows a parameterized policy π(𝑠|𝜃), where 𝜃 represents the parameters of the policy (such as weights in a neural network).
- The goal is to optimize the policy by updating 𝜃 in the direction that increases expected rewards.
- This is done using gradient ascent on the policy objective function.
Why Do We Need Policy Gradient Methods?
While value-based methods like Q-learning and DQN work well in many cases, they have limitations:
1. Continuous Action Spaces:
- Value-based methods struggle when actions are continuous (e.g., controlling a robot arm).
- Policy gradient methods can handle continuous action spaces by directly learning a probability distribution over actions.
2. Stochastic Policies:
- Value-based methods often learn deterministic policies (always selecting the best action).
- Policy gradients allow for stochastic policies, which help in exploration.
3. Better Performance in Complex Environments:
- In complex decision-making tasks (e.g., game playing, robotic control), learning a policy directly is often more efficient and stable than relying on value functions.
- Real-World Analogy:
Imagine you're learning how to ride a bicycle. - A value-based approach would involve estimating how good different balance strategies are and selecting the best one.
- A policy-based approach would directly learn how to adjust the balance using experience, without explicitly calculating a "value function."
Comparison of Policy Gradient vs. Value-Based Methods
| Feature | Policy Gradient Methods | Value-Based Methods (e.g., DQN) |
|---|---|---|
| Approach | Learns a policy directly | Learns a value function first |
| Action Space | Works well with continuous & discrete actions | Best for discrete actions |
| Determinism | Can be stochastic (better exploration) | Usually deterministic |
| Convergence | More stable in large problems | Can be unstable due to value estimation |
| Sample Efficiency | Less sample-efficient (high variance) | More sample-efficient (lower variance) |
Real-World Applications of Policy Gradient Methods
Policy gradients are used in several high-impact real-world applications:
1. Robotics
- Used in training robotic arms for precise movements (e.g., OpenAI’s dexterous hand).
- Enables real-time control of drones, self-balancing robots, and autonomous vehicles.
2. Game AI
- Used in AlphaGo (Google DeepMind), where policy gradients help select the best moves in Go, Chess, and StarCraft II.
- Reinforcement learning with policy gradients is widely used in video game bots (e.g., OpenAI Five for Dota 2).
3. Finance & Trading
- Algorithmic trading strategies use policy gradients to learn optimal investment decisions based on market data.
4. Healthcare
- Personalized treatment recommendations in healthcare use policy gradient-based sequential decision-making models.
Policy Gradient Theorem & REINFORCE Algorithm
In this module, we will dive deep into Policy Gradient Methods, a fundamental approach in reinforcement learning for training agents. We will cover:
What are Policy Gradient Methods?
Policy Gradient (PG) methods are a class of reinforcement learning algorithms that learn the policy directly instead of relying on a value function.
Key Idea:
- Instead of estimating a Q-value function Q(s,a), we parameterize the policy as πθ(a∣s).
- The policy πθ(a∣s) is represented by a neural network with learnable parameters θ.
- The goal is to find the best parameters θ that maximize the expected cumulative reward.
When to Use Policy Gradient Methods?
- When the action space is continuous (e.g., robotics, self-driving cars).
- When the optimal policy is stochastic (i.e., actions are probabilistic rather than deterministic).
Example: Training a Robot Arm
A robot arm needs to pick up an object.
- Discrete Action Space: Move left or right (use Q-learning, DQN).
- Continuous Action Space: Move fingers with precise force (use Policy Gradient Methods).
The Policy Gradient Theorem
The Policy Gradient Theorem provides a formula to compute the gradient of the expected reward with respect to the policy parameters.
The objective function we want to maximize is:
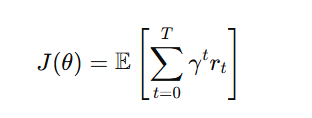
Gradient of the Policy Objective
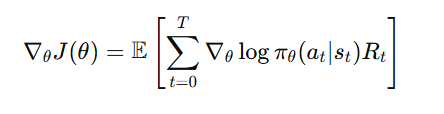
Explanation:
- We update the policy using the gradient ∇J(θ) to maximize rewards.
- The term log πθ(a | s) helps estimate how much an action contributes to the total reward.
- R_t is the cumulative reward obtained after taking action ata_t at state sts_t.
REINFORCE Algorithm (Monte Carlo Policy Gradient)
The REINFORCE Algorithm is the simplest Policy Gradient method. It uses Monte Carlo sampling to estimate the policy gradient.
Step-by-Step Breakdown of REINFORCE
1. Initialize the Policy Network
- The policy πθ(a∣s) is represented by a neural network.
- The network takes state (s) as input and outputs probabilities of actions.
2. Collect Trajectories (Episodes)
- Run the policy πθ(a∣s) for multiple episodes.
- Store all experiences (s,a,r) in a buffer.
3. Compute Returns for Each State
- Compute the cumulative reward G_t from time step t onward:
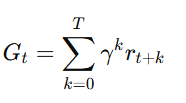
4. Update the Policy Parameters
- Adjust the policy parameters using gradient ascent:
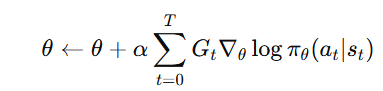
Intuition Behind the Update
- If an action leads to high rewards, increase its probability.
- If an action leads to low rewards, decreases its probability.
Advantages of REINFORCE
Works well with stochastic policies (useful in uncertain environments).
Handles continuous action spaces efficiently.
Optimizes policy directly, making it more flexible than value-based methods.
Limitations of REINFORCE
- High Variance in Gradient Estimates
- REINFORCE uses Monte Carlo sampling to estimate gradients, which introduces randomness and leads to high variance.
- This variance makes updates unstable, causing fluctuations in learning.
- Slow Convergence
- Since REINFORCE relies on full episodes before updating the policy, learning is slow and inefficient.
- It requires a large number of episodes to observe meaningful improvements.
- No Bootstrapping
- REINFORCE does not update its policy using partial experiences (i.e., it waits until the end of an episode).
- This means it does not reuse past experiences efficiently, unlike other RL methods such as Q-Learning or Actor-Critic.
Solutions to These Limitations
- Baseline Subtraction to Reduce Variance
- One way to reduce variance in gradient estimates is by using a baseline function.
- A common choice is the state-value function V(s), which estimates the expected return from a given state.
Instead of updating the policy based on raw returns Rt, we subtract a baseline to stabilize learning:
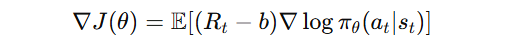
- The baseline does not change the expected gradient but reduces variance, leading to more stable updates.
- Use Actor-Critic Methods
- Actor-Critic methods combine the benefits of policy-based and value-based approaches.
- Instead of waiting until the end of an episode, the critic estimates value functions to provide better learning signals.
- The actor updates the policy based on feedback from the critic, making learning more sample-efficient and stable.
- This approach introduces bootstrapping, allowing learning from partial experiences rather than full episodes.
By applying these techniques, the weaknesses of REINFORCE can be mitigated, making RL training faster and more stable.
Actor-Critic Methods
Before diving into A2C and DDPG, let’s first understand the Actor-Critic (AC) framework.
What is an Actor-Critic Method?
- It combines value-based and policy-based methods.
- Uses two components:
- Actor: Learns the policy (πθ(a | s)) to decide which action to take.
- Critic: Learns the value function V(s)V(s) to evaluate how good a state is.
- The Critic guides the Actor to take better actions, improving training efficiency.
Why Actor-Critic?
Reduces the high variance in Policy Gradient Methods (like REINFORCE).
Converges faster than pure policy gradient methods.
Works well in continuous action spaces, unlike Q-learning.
Now, let’s explore A2C and DDPG, two popular Actor-Critic methods.
Advantage Actor-Critic (A2C)
Advantage Actor-Critic (A2C) is an improved version of Actor-Critic that stabilizes learning and reduces variance using the advantage function.
Key Idea
Instead of using the value function V(s) directly, we use the Advantage Function:
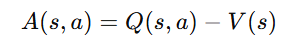
Why use the Advantage Function?
- It helps normalize the updates.
- It ensures that only the actions better than expected get reinforced.
Step-by-Step Breakdown of A2C
1. Initialize the Actor and Critic Networks
- Actor-network outputs πθ(a | s) (policy).
- Critic network estimates V(s) (state value).
2. Interact with the Environment
- Collect experiences (s,a,r,s′)
- Store them in a buffer.
3. Compute the Advantage Function
- Estimate the Advantage using the Critic:
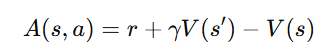
4. Update the Actor
- Actor updates its policy using policy gradient:
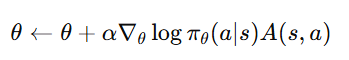
5. Update the Critic
- Critic minimizes the Mean Squared Error (MSE) loss:
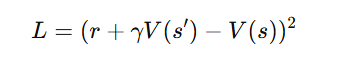
Deep Deterministic Policy Gradient (DDPG)
DDPG is an off-policy Actor-Critic method designed for continuous action spaces.
Key Idea
- Uses a deterministic policy (unlike A2C, which is stochastic).
- Uses two networks:
- Actor: Learns a deterministic policy μθ(s).
- Critic: Estimates the Q-value Q(s,a).
- Uses Experience Replay and Target Networks to stabilize learning.
Step-by-Step Breakdown of DDPG
1. Initialize the Actor and Critic Networks
- The actor outputs a continuous action a=μθ(s).
- Critic estimates Q-values Q(s,a)
2. Use Experience Replay
- Store experiences (s,a,r,s′) in a buffer.
- Randomly sample mini-batches to break correlation.
3. Update the Critic
- Compute target Q-values:
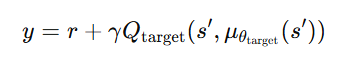
- Minimize the loss:
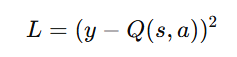
4. Update the Actor
- Compute policy gradient using Deterministic Policy Gradient (DPG):
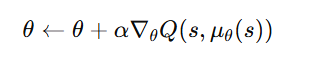
5. Update the Target Networks
- Use soft updates to stabilize training:
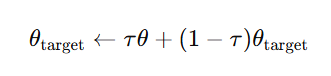
where τ is a small value (e.g., 0.001).
Key Differences Between A2C and DDPG
| Feature | A2C (Advantage Actor-Critic) | DDPG (Deep Deterministic Policy Gradient) |
|---|---|---|
| Action Space | Discrete & Continuous | Continuous only |
| Policy Type | Stochastic | Deterministic |
| Exploration | Uses randomness in policy | Uses Ornstein-Uhlenbeck noise |
| Sample Efficiency | On-policy (less efficient) | Off-policy (more efficient) |
| Stability | More stable than REINFORCE | Uses Target Networks & Experience Replay |
Advantages & Limitations of A2C & DDPG
Advantages of A2C
More stable than REINFORCE.
Works in both discrete and continuous action spaces.
Reduces variance using Advantage Function.
Limitations of A2C
Still suffers from high variance.
Requires on-policy updates (less efficient).
Advantages of DDPG
Works well in continuous action spaces (robotics, autonomous driving).
Uses Experience Replay & Target Networks to stabilize training.
More sample efficient than A2C.
Limitations of DDPG
Sensitive to hyperparameters (e.g., learning rate, noise).
Requires careful exploration strategies (Ornstein-Uhlenbeck noise).
Key Takeaways
- Policy Gradient Methods directly learn an optimal policy instead of relying on value functions, making them suitable for complex RL tasks like robotics and autonomous driving.
- Difference from Value-Based Methods:
- Value-Based (e.g., DQN): Learns a value function first, then derives a policy.
- Policy-Based (Policy Gradients): Learns a policy directly, making it more effective in continuous and stochastic environments.
- Advantages of Policy Gradient Methods:
- Handles continuous action spaces (e.g., robotic control).
- Supports stochastic policies, improving exploration.
- More stable in complex environments where value-based methods struggle.
- Policy Gradient Theorem & REINFORCE Algorithm:
- Uses gradient ascent to optimize policy parameters.
- The REINFORCE algorithm (Monte Carlo Policy Gradient) learns policies by maximizing expected rewards.
- Limitations of REINFORCE: High variance, slow convergence, and no bootstrapping.
- Solutions to REINFORCE’s Limitations:
- Baseline Subtraction: Reduces variance using a state-value function V(s).
- Actor-Critic Methods: Combines value-based (critic) and policy-based (actor) learning for faster and more stable training.
- Actor-Critic Methods (A2C & DDPG):
- Advantage Actor-Critic (A2C): Uses an advantage function to stabilize training.
- Deep Deterministic Policy Gradient (DDPG): An off-policy method for continuous action spaces, leveraging experience replay and target networks for stability.
- Key Differences Between A2C & DDPG:
- A2C: On-policy, stochastic, uses an advantage function.
- DDPG: Off-policy, deterministic, uses replay buffer and soft target updates.
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
