Introduction to Reinforcement Learning (RL)

Reinforcement Learning (RL) is a type of machine learning where an agent learns by interacting with an environment to maximize a cumulative reward. Unlike supervised learning, where labeled data is provided, RL relies on exploration and exploitation to discover optimal strategies.

One of the most popular RL algorithms is Q-learning. This algorithm helps an agent learn optimal actions to take in various states to maximize long-term rewards. This blog will explore Q-Learning in-depth, its working principles, and practical implementations.

What is Q-Learning?

Q-learning is an off-policy, model-free reinforcement learning algorithm that seeks to find the optimal Q-values for a given environment. The Q-value represents the expected future rewards for taking a particular action in a given state.

Key Components of Q-Learning

1. Agent: The entity that interacts with the environment and learns from rewards. The agent takes actions to explore the environment and update its knowledge based on received rewards.
2. Environment: The space where the agent operates. It defines the set of states, possible actions, and the rules governing state transitions and rewards.
3. State (S): A representation of the agent's current situation within the environment. Each state provides information that helps the agent decide on the next action.
4. Action (A): The set of possible moves the agent can make. The agent selects an action based on its current state and past experiences.
5. Reward (R): The feedback received after performing an action. Rewards can be positive or negative, guiding the agent toward desirable behaviors and away from suboptimal actions.
6. Q-Table (Q(S, A)): A table where each state-action pair is assigned a value representing the expected future reward. The Q-table is updated iteratively as the agent interacts with the environment, refining its understanding of the best actions to take in different states.

Methods for Determining Q-Values

There are two primary methods for determining Q-values:

1. Temporal Difference (TD): This method calculates Q-values by comparing the current state and action values with the previous ones. It updates the Q-value incrementally as the agent interacts with the environment, making learning more efficient.
2. Bellman’s Equation: Invented by Richard Bellman in 1957, this recursive formula is used to calculate the value of a given state and determine its optimal position. It plays a crucial role in Q-learning by providing a mathematical foundation for decision-making in Markov Decision Processes (MDP).

Bellman’s Equation

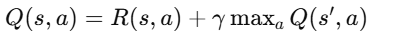
Where:

• Q(s,a): The Q-value for a given state-action pair.
• R(s,a): The immediate reward for taking action a in state s.
• γ (gamma): The discount factor, representing the importance of future rewards.
• max Q(s',a): The maximum Q-value for the next state s' over all possible actions.

The Bellman equation ensures that Q-values incorporate both immediate and future rewards, allowing the agent to learn an optimal policy over time.

What is a Q-Table?

A Q-Table is a matrix that stores Q-values for each state-action pair. It helps the agent determine the best possible action in a given state by looking up the highest Q-value.

Structure of a Q-Table:

• Rows represent different states.
• Columns represent different actions.
• Cell values store expected future rewards for a given state-action pair.

Over time, as the agent explores the environment and updates Q-values using the Bellman equation, the Q-table converges to an optimal policy.

How Q-Learning Works

Q-Learning follows an iterative process where the agent explores the environment, updates its Q-values, and learns an optimal policy over time. The process follows these steps:

Step 1: Initialize Q-Table

A Q-table is initialized with arbitrary values (often zeros). It has rows representing states and columns representing actions.

Step 2: Choose an Action Using an Exploration Strategy

The agent selects an action using an epsilon-greedy policy, which balances exploration and exploitation:

• With probability ε (epsilon), the agent explores by choosing a random action.
• With probability 1 - ε, the agent exploits by choosing the action with the highest Q-value.

Step 3: Take Action and Observe Reward

After selecting an action, the agent interacts with the environment and receives a reward based on the outcome.

Step 4: Update Q-Value Using the Bellman Equation

The Q-value is updated using the Q-Learning update rule:

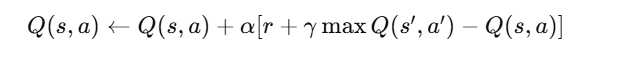
where:

• Q(s, a) = Current Q-value of state-action pair.
• α (alpha) = Learning rate (controls the update intensity).
• r = Reward received.
• γ (gamma) = Discount factor (determines importance of future rewards).
• max Q(s', a') = Maximum future Q-value for the next state.

Step 5: Repeat Until Convergence

The agent continues to interact with the environment and update its Q-table until it converges to an optimal policy.

Applications of Q-Learning

Q-Learning has various real-world applications, including:

1. Game AI: Used in video games and board games (e.g., AlphaGo) to develop intelligent strategies.
2. Robotics: Helps robots learn to navigate and perform tasks autonomously.
3. Self-Driving Cars: Assists in decision-making for lane changing, braking, and route optimization.
4. Finance: Used for stock trading and portfolio management by learning optimal investment strategies.
5. Healthcare: Aids in treatment planning and optimizing medical resource allocation.
6. Network Optimization: Helps optimize routing protocols in communication networks.

Advantages of Q-Learning

1. Model-Free: Q-Learning does not require prior knowledge of the environment.
2. Off-Policy: Can learn from stored experiences without directly interacting with the environment.
3. Guaranteed Convergence: Given enough training time and a proper learning rate, Q-Learning will find the optimal policy.

Limitations of Q-Learning

1. Inefficient for Large State Spaces: As the number of states increases, the Q-table grows exponentially.
2. Slow Convergence: If the learning rate or exploration strategy is not optimized, learning can be slow.
3. Not Suitable for Continuous Spaces: Q-Learning struggles with environments having continuous state-action spaces.

Key Takeaways:

1. Reinforcement Learning (RL) – A machine learning approach where an agent learns by interacting with an environment to maximize rewards.
2. Q-Learning – An off-policy, model-free RL algorithm that finds the optimal action-selection policy using Q-values.
3. Key Components – Includes agent, environment, states, actions, rewards, and a Q-table.
4. Bellman’s Equation – A fundamental formula used to update Q-values and optimize decision-making.
5. Q-Table – A matrix storing Q-values for state-action pairs, helping the agent determine the best actions.
6. Exploration vs. Exploitation – Balances learning new actions (exploration) and using known optimal actions (exploitation).
7. Update Rule – Q-values are updated iteratively using the Bellman equation to improve the policy.
8. Applications – Used in gaming, robotics, self-driving cars, finance, healthcare, and network optimization.
9. Advantages – Model-free, off-policy learning with guaranteed convergence to an optimal solution.
10. Limitations – Inefficient for large state spaces, slow convergence, and struggles with continuous state-action spaces.
    
    Next Blog- Python implementation of Q-Learning