What is a Markov Decision Process?

Introduction

Markov Decision Process (MDP) is a mathematical framework used for decision-making in situations where outcomes are partly random and partly controlled by a decision-maker. MDPs are fundamental in Reinforcement Learning (RL) and provide a formalized way to model environments where an agent interacts with a system to achieve a goal. They are widely used in robotics, economics, automated control systems, and artificial intelligence.

Components of Markov Decision Process

A Markov Decision Process (MDP) is a mathematical framework used to model decision-making in stochastic environments. It consists of five key components, which define how an agent interacts with its environment to achieve its goal.

1. States (S)

The state represents the current situation of the environment that the agent observes. It provides all the necessary information about the environment at a given time step. The set of all possible states is denoted as S.

For example, in a self-driving car scenario, a state could include the car’s current position, speed, nearby obstacles, and traffic signals.

2. Actions (A)

An action is a decision the agent makes at a given state. The set of all possible actions is denoted as A. The agent chooses an action based on its current state to maximize future rewards.

For instance, in a chess game, actions could include moving a piece to a different square. In a robot navigation problem, actions could be moving forward, turning left, or turning right.

3. Transition Probability (P)

The transition probability represents the likelihood that taking an action in a particular state will lead to another state. It is denoted as:

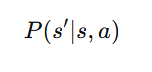
where:

• s is the current state,
• a is the action taken, and
• s′ is the next state.

If the environment is deterministic, the transition is fixed (i.e., taking an action in a state always leads to the same next state). If the environment is stochastic, taking an action might lead to different next states with varying probabilities.

For example, in a board game, rolling a dice leads to different outcomes with certain probabilities.

4. Reward Function (R)

The reward function defines the immediate reward an agent receives for taking an action in a given state. It is denoted as:

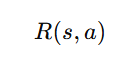
where:

• R(s,a)  is the reward received for taking action aaa in state sss.

The reward guides the agent’s learning process by reinforcing good actions and discouraging bad ones.

For example, in a game scenario, winning a round might provide a reward of +10 points, while losing might result in a penalty of -5 points.

5. Discount Factor (γ)

The discount factor (γ\gammaγ) determines how much the agent values future rewards compared to immediate rewards. It is a number between 0 and 1:

• If γ = 0, the agent only cares about immediate rewards.
• If γ = 1, the agent values future rewards as much as immediate ones.
• A typical choice is γ = 0.9, meaning future rewards are considered but slightly less than immediate rewards.

For example, in investment planning, an agent might value long-term gains over short-term profits, and the discount factor helps model this preference.

Markov Property

The Markov Property is a fundamental concept in probability theory and reinforcement learning. It states that the future state of an environment depends only on its current state and action, and not on any past states or actions. This memoryless property simplifies decision-making, allowing for efficient modeling of stochastic environments using Markov Decision Processes (MDPs).

Mathematically, the Markov Property can be expressed as:

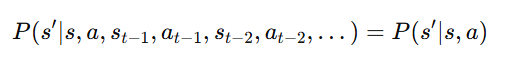
This equation states that the probability of reaching the next state s′ depends only on the current state s and the action a, irrespective of past states (st−1,st−2,…) and actions (at−1,at−2,…at-1, at-2, …).

Why is the Markov Property Important?

1. Simplifies Computation: Since the decision-making process does not depend on past states, the computational complexity is significantly reduced, making MDPs more efficient to solve.
2. Efficient Modeling: Many real-world systems exhibit the Markov Property, allowing them to be accurately represented and solved using MDPs.
3. Reinforcement Learning Foundation: Most RL algorithms, such as Q-learning and Deep Q-Networks (DQNs), assume the Markov Property to estimate optimal policies and value functions.
4. Predictability in Decision-Making: The agent only needs the current state to make an optimal decision, reducing unnecessary dependencies on historical data.

Relevance of Markov Decision Processes (MDPs) to Reinforcement Learning

Markov Decision Processes (MDPs) serve as the mathematical foundation of Reinforcement Learning (RL). They provide a structured framework for modeling decision-making problems where an agent interacts with an environment to achieve a goal. Since most RL problems involve uncertainty and sequential decision-making, MDPs are crucial for defining how an agent should behave optimally in such environments.

How MDPs Relate to Reinforcement Learning

1. Defines the Learning Problem
   • In RL, an agent learns by taking actions in an environment and receiving rewards.
   • MDPs formalize this interaction using states (S), actions (A), transition probabilities (P), rewards (R), and a discount factor (γ).
   • This structure helps in formulating RL problems mathematically and finding optimal policies.
2. Decision-Making in Uncertain Environments
   • Many real-world applications involve uncertainty (e.g., robotics, finance, healthcare).
   • MDPs help model these stochastic environments where the outcome of an action is not deterministic but follows a probability distribution.
   • RL algorithms rely on MDPs to handle uncertainty efficiently while learning optimal policies.
3. Policy Optimization
   • In RL, the goal is to find an optimal policy (π)—a strategy that tells the agent which action to take in each state.
   • MDPs provide the foundation for value-based RL (e.g., Q-learning) and policy-based RL (e.g., Policy Gradient Methods) to optimize decision-making.
4. Reward Maximization
   • Reinforcement Learning is based on maximizing cumulative rewards over time.
   • The reward function (R) in an MDP defines immediate rewards for actions, while the discount factor (γ) balances short-term vs. long-term rewards.
   • RL algorithms use MDPs to evaluate expected future rewards and adjust actions accordingly.
5. Value Functions and Bellman Equations
   • RL uses value functions (V) and Q-values (Q) to estimate the desirability of states and actions.
   • These functions are based on Bellman equations, which are derived from MDPs.
   • Dynamic Programming techniques like Value Iteration and Policy Iteration help solve MDPs and guide RL algorithms.

How MDPs Help in Reinforcement Learning Algorithms

• Model-Free RL (e.g., Q-learning, Deep Q Networks)
  • These algorithms do not explicitly model transition probabilities (P).
  • Instead, they learn through experience by trial and error while interacting with the environment.
• Model-Based RL
  • Some RL methods use an estimated model of the environment (P and R) to plan future actions.
  • This helps in faster learning and better decision-making in complex tasks.

Bellman Equations

The Bellman equations are fundamental recursive equations in Reinforcement Learning (RL) that define the relationship between the value of a state and the values of its possible future states. They are used to evaluate policies and compute optimal policies in Markov Decision Processes (MDPs).

1. Bellman Expectation Equation

The Bellman Expectation Equation expresses the value function Vπ(s)  of a policy π in terms of the expected rewards and future values:

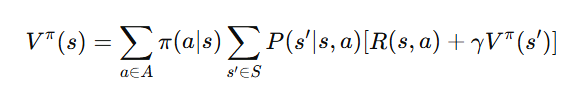
Explanation:

• Vπ(s) represents the expected return (sum of future rewards) from state sss when following policy π.
• The sum over aaa accounts for all possible actions, weighted by the probability π(a∣s) of selecting each action under the policy.
• P(s′∣s,a) is the transition probability of reaching state s′ after taking action a in state s.
• R(s,a) is the immediate reward received for taking action a in state s.
• γ(discount factor) determines how much future rewards contribute to the present value.

2. Bellman Optimality Equation

The Bellman Optimality Equation defines the optimal value function V∗(s), which represents the maximum achievable reward from any state when following the best possible policy:

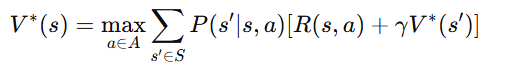
Explanation:

• Instead of summing over all actions according to a policy π, the optimal equation chooses the action that maximizes expected rewards.
• This equation is used to compute the optimal policy π∗ that maximizes the long-term reward.

3. Bellman Equation for Q-Values (Q-function)

The Q-function represents the expected reward when taking a specific action in a given state and then following the optimal policy. The Bellman equation for Q-values is:

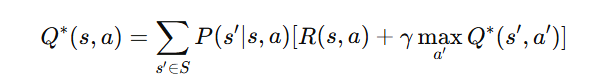
Explanation:

• Q∗(s,a) represents the best possible reward from state s when taking action a.
• The equation finds the expected future reward by summing over all possible next states s′.
• The maximum over a′ ensures that the optimal action is chosen at the next step.

Why Are Bellman Equations Important?

Foundation for Dynamic Programming: Used in Value Iteration and Policy Iteration algorithms.
Core of Model-Free RL Methods: Used in Q-learning and Deep Q Networks (DQN).
 Help in Policy Evaluation & Improvement: They guide agents in making optimal decisions.

Solving MDPs in Reinforcement Learning

Solving a Markov Decision Process (MDP) in Reinforcement Learning (RL) means finding an optimal policy π∗ that maximizes the cumulative reward over time. This process involves evaluating and improving policies using various techniques, such as Dynamic Programming (DP), Monte Carlo methods, and Temporal Difference (TD) learning.

Methods for Solving MDPs

1. Dynamic Programming (DP) Methods

Dynamic Programming techniques solve MDPs using Bellman equations by iteratively updating value functions. These methods assume a known environment model (transition probabilities P(s′∣s,a) and rewards R(s,a)

A. Policy Evaluation

• Computes the value function Vπ(s) for a given policy π.

• Uses the Bellman Expectation Equation:

  

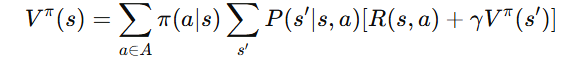
• Iteratively updates the value function until convergence.

B. Policy Improvement

• Once Vπ(s) is estimated, the policy is updated to maximize future rewards

  

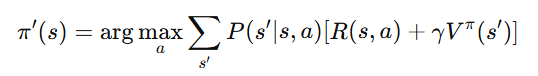
• This step improves the policy by choosing actions that lead to higher rewards.

C. Policy Iteration

• Alternates between policy evaluation and policy improvement until the optimal policy π∗ is found.

D. Value Iteration

• Instead of full policy evaluation, this method directly updates value functions using the Bellman Optimality Equation:

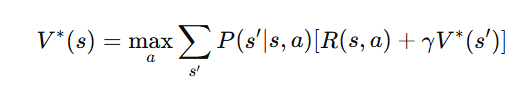
• his approach quickly converges to the optimal policy.

2. Model-Free Methods

When the transition probabilities P(s′∣s,a) are unknown, model-free reinforcement learning methods are used.

A. Monte Carlo Methods

• Learn from complete episodes (sequences of state-action-reward transitions).
• Estimate the value function based on actual returns received from multiple episodes.
• Suitable for environments where episodes naturally end (e.g., games like chess).

B. Temporal Difference (TD) Learning

• Updates value functions before an episode ends, making it more efficient than Monte Carlo methods.

• Uses the equation: 

  

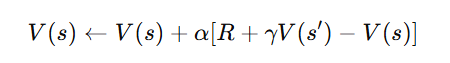
• Q-learning (off-policy) and SARSA (on-policy) are common TD learning algorithms.

3. Policy-Based Methods

• Instead of learning value functions, these methods directly optimize the policy.

A. Policy Gradient Methods

• Learn policies directly by adjusting parameters to maximize expected rewards.
• Use gradient ascent with an objective function:

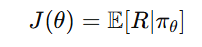
• where θ are policy parameters.
• Example: REINFORCE algorithm, Actor-Critic methods.

B. Actor-Critic Algorithms

• Combine value-based and policy-based approaches.
• Actor updates policy parameters using gradient ascent.
• Critic evaluates actions by estimating value functions.

• Example: Deep Deterministic Policy Gradient (DDPG).

   

Applications of MDP

MDPs are widely used in various fields:

• Robotics: Decision-making for autonomous robots.
• Healthcare: Optimizing treatment plans.
• Finance: Portfolio management.
• Supply Chain Management: Inventory optimization.

Key Takeaways: 

• Framework for Decision-Making:
  • MDPs model environments where outcomes depend on both chance and the actions of a decision-maker.
• Core Components:
  • States (S): Current conditions of the environment.
  • Actions (A): Choices available to the agent.
  • Transition Probabilities (P): Likelihood of moving between states given an action.
  • Reward Function (R): Immediate feedback from actions.
  • Discount Factor (γ): Balances the value of immediate and future rewards.
• Markov Property:
  • Future states depend only on the current state and action, not on past history.
• Bellman Equations:
  • Form the basis for evaluating and improving policies by relating state values to future rewards.
• Solving MDPs:
  • Techniques include Dynamic Programming (Policy Iteration, Value Iteration), Monte Carlo methods, Temporal Difference learning, and Policy Gradient methods.
• Applications:
  • Widely used in robotics, healthcare, finance, supply chain management, and more.
• Reinforcement Learning Connection:
  • MDPs provide the mathematical foundation for RL algorithms to learn optimal decision-making policies.

Next Blog- Markov Decision Process (MDP) – Step-by-Step Python Implementation