Mathematics for Machine Learning: Linear Algebra Basics
Machine learning relies on mathematics to make sense of data, and one of the most important mathematical tools is linear algebra. From representing data in high-dimensional spaces to enabling optimizations, linear algebra plays a crucial role in machine learning algorithms.
In this blog, we’ll break down the essential concepts of linear algebra that power machine learning, ensuring you gain a practical understanding. Let’s dive in!
Why is Linear Algebra Important for Machine Learning?
Linear algebra enables the mathematical representation of machine learning processes. It helps describe relationships between variables, perform computations, and optimize models efficiently. Here are some of its applications:
- Data Representation: Data is often stored as vectors (1D) or matrices (2D). For instance, a dataset with 100 samples and 10 features is represented as a 100×10100 \times 10 matrix.
- Transformations: Algorithms like PCA (Principal Component Analysis) use matrix operations to scale, rotate, or project data into lower-dimensional spaces.
- Optimization: Gradient descent, used to minimize errors in models, calculates gradients using linear algebra.
- Model Computations: Deep learning heavily relies on matrix multiplications for forward propagation and backpropagation.
Without linear algebra, machine learning as we know it would not exist.
Core Concepts of Linear Algebra
Here are the foundational building blocks of linear algebra and how they connect to machine learning.
1. Scalars, Vectors, Matrices, and Tensors
These four fundamental components are the building blocks of data representation in machine learning. Understanding these concepts is essential to comprehend how machine learning algorithms operate on data. Let’s break each one down in detail.
a. Scalars
A scalar is the simplest form of data representation in linear algebra. It is a single numerical value, which can be an integer, floating-point number, or any other type of single value. Scalars are used to represent quantities that don’t have any direction or dimensionality.
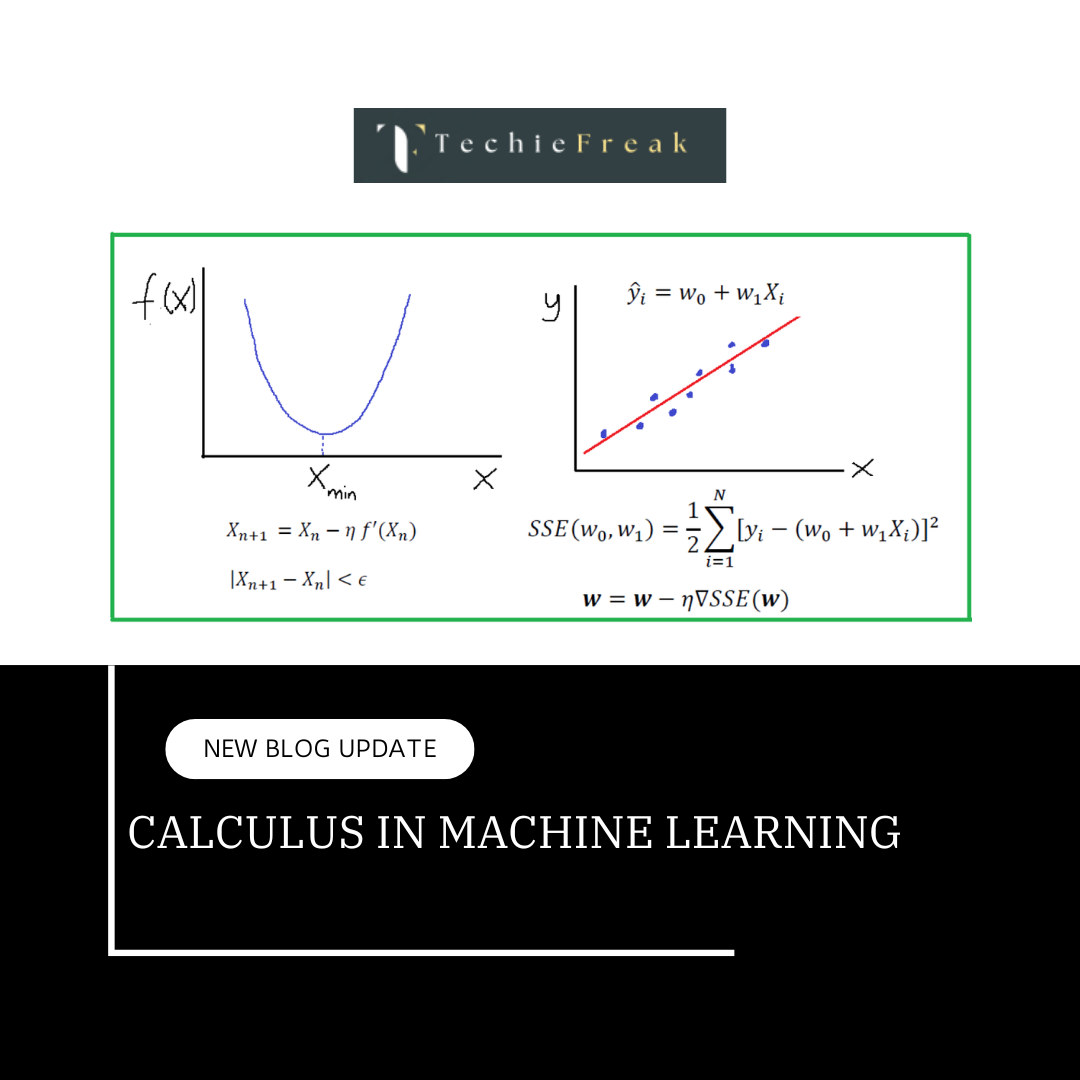
- Definition: A scalar s is just a single number.
- Examples in Machine Learning:
- Weights and Biases: In machine learning models, weights and biases are often scalars, especially in simpler models.
- Hyperparameters: Learning rate (η\etaη), regularization strength (λ\lambdaλ), and dropout rate are all examples of scalars.
- Loss Value: The output of a loss function, which evaluates how well a model is performing, is typically a scalar.
Mathematical Example:
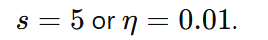
b. Vectors
A vector is a one-dimensional array of numbers that represents a point in space or a direction. In machine learning, vectors are commonly used to store data points, features, or model parameters.
- Definition: A vector v\mathbf{v}v is an ordered list of numbers, typically represented as a column vector or a row vector.
Notation:
A column vector is written as: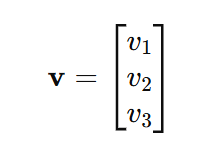
A row vector is written as:
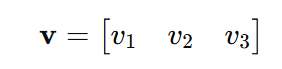
- Examples in Machine Learning:
Feature Vectors: A single data point with multiple features can be represented as a vector.
Example: For a dataset with features like height, weight, and age, a single instance might be represented as:
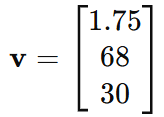
Model Parameters: In logistic regression, the weights of the model are stored as a vector.
Vector Operations
Vector operations form the foundation of numerous machine learning algorithms and are critical in linear algebra, physics, and computer science. Let’s explore the most common vector operations in detail:
1. Addition and Subtraction
Vectors of the same dimension can be added or subtracted element-wise. These operations are used to combine or differentiate vectors in space.
Addition:
If v1 and v2 are two vectors of the same size, their sum v1+v2 is computed as: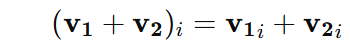
Subtraction:
Similarly, the difference v1−v2 is computed as: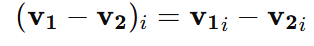
Example:
Let: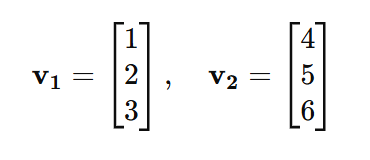
Addition:
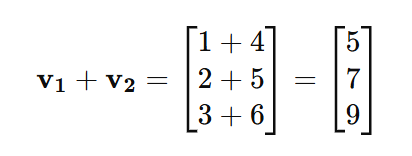
Subtraction:
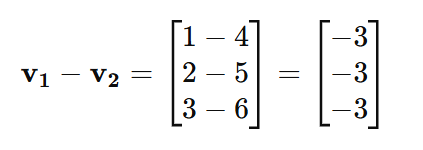
2. Scalar Multiplication
Scalar multiplication scales a vector by multiplying each of its components by a scalar. This operation is used to resize vectors while maintaining their direction.
Definition:
If v is a vector and c is a scalar, then the scaled vector c⋅v is computed as: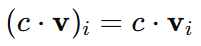
Example:
Let: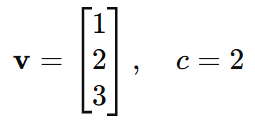
Scalar Multiplication:
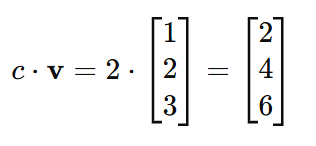
3. Dot Product
The dot product of two vectors results in a scalar that measures the alignment or similarity between the two vectors. It is used in various machine learning applications, such as computing projections and similarity measures.
Formula:
_1735388227.png)
Geometric Interpretation:
The dot product can also be expressed in terms of the magnitudes of the vectors and the cosine of the angle θ between them: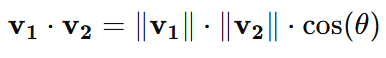
If θ=0∘ , the vectors are aligned, and the dot product is maximal.
If θ=90∘ , the vectors are perpendicular, and the dot product is zero.
Example:
Let: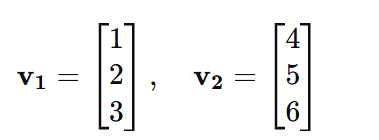
Compute the dot product:
_1735388881.png)
Result: v1⋅v2 = 32
4. Cross Product
The cross product is specific to 3D vectors and results in a vector that is perpendicular to the two input vectors. It is commonly used in physics and 3D geometry.
Definition:
_1735389031.png)
Geometric Interpretation:
The magnitude of the cross-product represents the area of the parallelogram formed by v1 and v2. The direction of the resulting vector is determined by the right-hand rule.Example:
Let: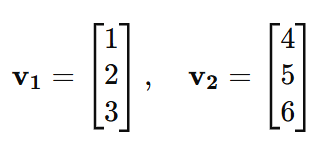
Compute the cross-product:
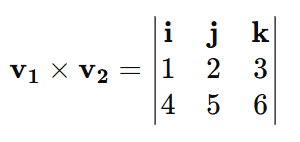
Expanding the determinant:
_1735390265.png)
Result:
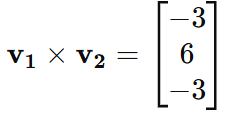
c. Matrices
A matrix is a two-dimensional array of numbers, organized into rows and columns. In machine learning, matrices are used to represent datasets, transformations, or model parameters.
Definition: A matrix A is a rectangular array of numbers with m rows and n columns, denoted as :
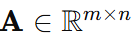
Notation
A matrix with 2 rows and 3 columns is written as: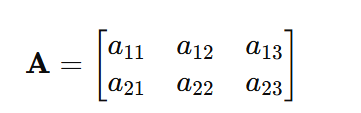
- Examples in Machine Learning:
Datasets: A dataset with m samples and n features can be represented as a matrix where each row is a data point and each column is a feature.
Example: For a dataset with 4 samples and 3 features: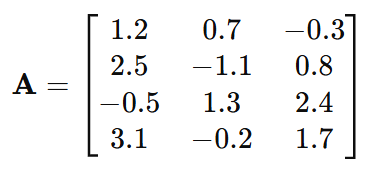
- Weights in Neural Networks: The weights between layers in a neural network are stored as matrices.
Matrix Operations
Matrices are essential in many computational tasks, including graphics, physics, and machine learning. Here, we explore fundamental operations that can be performed on matrices.
1. Matrix Addition and Subtraction
Matrix addition and subtraction involve combining two matrices of the same dimension by performing element-wise operations.
Definition: For two matrices A and B of dimensions m×n, their sum or difference is given as:
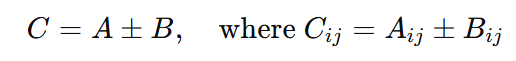
_1735390599.png)
Example:
_1735390358.png)
Note: Addition and subtraction can only be performed if both matrices have the same dimensions.
2. Scalar Multiplication
Scalar multiplication involves multiplying each element of a matrix by a scalar value.
Definition: For a matrix A of dimension m×n and a scalar k, the result B is given as:
_1735390389.png)
Applications:
- Scaling transformations in graphics.
- Adjusting weights in neural networks.
3. Matrix Multiplication
Matrix multiplication combines the rows of the first matrix with the columns of the second matrix. It is not element-wise and requires specific dimensions.
Definition: If A is an m×n matrix and B is an n×p matrix, their product CCis an m×p matrix, where:
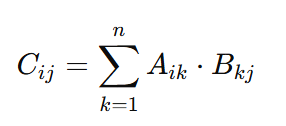
Here, Cij is the dot product of the i-th row of A and the j-th column of B.
Example:
_1735390440.png)
Applications:
- Neural network computations.
- Transformations in computer graphics.
- Solutions to systems of linear equations.
4. Transpose
The transpose of a matrix flips its rows and columns.
Definition: For a matrix A of dimension m×n, the transpose A^T is of dimension n×m, where:
Example:
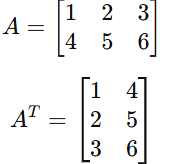
Applications:
- Finding eigenvectors and eigenvalues.
- Symmetric matrix analysis.
- Simplifying linear equations.
- Understanding these operations forms the basis of linear algebra, which is widely used in machine learning, physics, and engineering disciplines.
d. Tensors
A tensor is a generalized concept of scalars, vectors, and matrices that extends to higher dimensions. While a vector is a 1D tensor and a matrix is a 2D tensor, tensors can have three or more dimensions.
- Definition: A tensor is an n-dimensional array of numbers. The rank of a tensor indicates the number of dimensions.
- Examples in Machine Learning:
Image Data: In deep learning, an RGB image is represented as a 3D tensor:
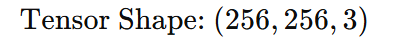
where the dimensions represent height, width, and color channels.
Video Data: A video clip can be represented as a 4D tensor:
_1735388142.png)
- Visualization:
- A scalar is a single point.
- A vector is a line of points.
- A matrix is a grid of points.
- A tensor extends this grid into higher dimensions.
- Operations:
Tensors can be manipulated using element-wise operations, slicing, and reshaping. Libraries like TensorFlow and PyTorch provide tools to handle tensor operations efficiently.
4. Linear Transformations in Machine Learning
Linear transformations are essential in understanding how data points are manipulated and represented in space using matrices. In machine learning, they play a significant role in preprocessing, feature engineering, and deep learning.
Definition of Linear Transformation
A linear transformation maps a vector v in one space to another vector v′ in a different space using a matrix A:
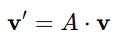
Here:
- v is the input vector.
- v′ is the transformed vector.
- A is the transformation matrix.
Common Linear Transformations
Scaling: Scaling increases or decreases the size of a vector or dataset by multiplying it with a scalar matrix.
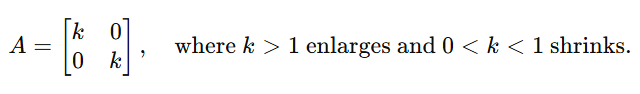
Example:
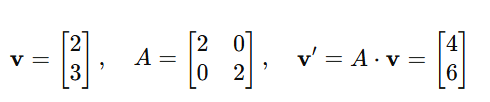
Rotation: Rotation rotates a vector around the origin. The transformation matrix depends on the angle θ:
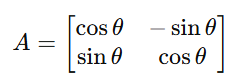
Example: Rotating a point (1, 0) by 90°:
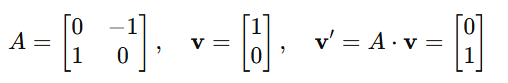
- Translation: While not strictly linear, translations shift a vector by adding a constant vector. This is often implemented using homogeneous coordinates in computer graphics.
Shear: Shearing distorts a vector such that it is displaced in one direction proportional to its magnitude in another direction.
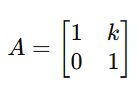
Here, k controls the degree of shear.
Applications in Machine Learning
- Data Preprocessing:
- Scaling features to a uniform range (e.g., normalizing data).
- Transforming images for augmentation (rotation, scaling, shearing).
- Feature Transformation:
- Converting data points into a new space where patterns are more apparent.
- Principal Component Analysis (PCA) involves linear transformations to reduce dimensionality.
- Neural Networks:
- Linear layers in neural networks apply transformations via weight matrices.
5. Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors provide a deeper understanding of matrix transformations and are pivotal in many machine learning applications, such as dimensionality reduction and optimization.
Definition
For a square matrix A, if there exists a vector v and a scalar λ such that:
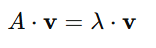
- v is the eigenvector, representing a direction that remains invariant under the transformation.
- λ is the eigenvalue, representing the scaling factor along the eigenvector.
Geometric Interpretation
- Eigenvectors are directions that do not change direction during a transformation, only their magnitude is scaled.
Eigenvalues describe how much the eigenvectors are stretched or compressed.
_1735390546.png)
Properties
- Eigenvectors corresponding to distinct eigenvalues are linearly independent.
- The determinant of A−λI=0 yields the eigenvalues, where I is the identity matrix.
Applications in Machine Learning
- Principal Component Analysis (PCA):
- PCA uses eigenvectors and eigenvalues of the covariance matrix to identify directions (principal components) that maximize variance.
- Data is projected onto the top k eigenvectors to reduce dimensionality.
- Stability Analysis:
- Eigenvalues help analyze the stability of dynamic systems in control and optimization.
- Spectral Clustering:
- Eigenvectors of similarity matrices are used for clustering in graph-based learning.
- Neural Networks:
- Eigenvalues of weight matrices are used to study network behavior and convergence.
Example in PCA
- Compute the covariance matrix CC of a dataset.
- Find eigenvalues and eigenvectors of CC.
- Choose the top kk eigenvectors corresponding to the largest eigenvalues.
- Project the dataset onto these kk-dimensional subspaces.
Eigenvalues and eigenvectors are fundamental to understanding the mechanics of linear transformations and play a critical role in reducing computational complexity while preserving important data characteristics.
6. Practical Applications
- PCA (Principal Component Analysis): Uses eigenvectors and eigenvalues for dimensionality reduction.
- Neural Networks: Relies on matrix operations for efficient data flow.
- Linear Regression: Uses matrices for fitting models.
Key Takeaways
- Linear algebra is essential for understanding and optimizing machine learning models.
- Core operations, such as matrix multiplication and dot products, are fundamental to algorithms.
- Concepts like eigenvalues are critical for dimensionality reduction.
- Regular practice with tools like NumPy strengthens these concepts.
Decode uncertainty with confidence! Our next blog delves into Probability and Statistics, equipping you with the mathematical tools essential for understanding and building robust Machine Learning models.
Next Topic : Probability and Statistics